メトロポリス・ヘイスティングス法の解説
汎用的なサンプリングアルゴリズムであるメトロポリス・ヘイスティングス法について解説します. ただし数学的な証明等は行わず, 事実を述べるだけにします.
(少しずつコード例や実験例, 出典を加筆していきたい)
はじめに
ベイズ推論において事後分布が解析的に計算できない場面というのは往々にして存在します. その際のひとつの解決策がサンプリングです.
事後分布に従うサンプルを得ることで, 事後分布について分かったことにしようということです.
今回はマルコフ連鎖モンテカルロ法と呼ばれる大きなアルゴリズム群の中でも汎用的な, メトロポリス・ヘイスティングス法について解説します.
文章中ではめんどいのでMH法と書くことにします.
概要
まずは記号の設定です.
- \(\pi(x)\): 知りたい分布の確率密度関数. 正規化係数のみ計算できない.
- \(\pi_*(x)\): \(\pi(x)\) の正規化係数を除いた部分.
ベイズ推論においては事後分布の正規化係数のみ分からないという場面はよく出てきます. したがってMH法をベイズ推論において使う場合, 正規化係数以外は計算できるという条件は足かせにはなりません.
さっそくですが, MH法は以下のステップからなります.
- \(x_t\) まで得られたとする.
- 提案分布 \(q(x \mid x_t)\) から \(x_{t+1}\) の候補 \(x_*\) をサンプルする.
- \(\alpha(x_t, x_*)\) の確率で \(x_*\) を受理し, \(x_{t+1} = x_*\) とする.
- \(x_*\) が棄却されたら \(x_{t+1} = x_t\) とする.
ただし受理確率 (acceptance rate) \(\alpha(x_t, x_*)\) は以下で定義されます.
\[ \alpha(x_t, x_*) = \min\left\{\frac{\pi(x_*)q(x_t \mid x_*)}{\pi(x_t)q(x_* \mid x_t)}, 1\right\} \]
\(\pi\) と \(\pi_*\) は定数倍違うだけなので, 上の式の \(\pi\) の代わりに \(\pi_*\) を使うことができますね. ここで, 正規化係数は分かっていなくてもいいというのが効いてきます.
以上の一連のステップにより, \(x_0, x_1, \ldots\) は \(\pi(x)\) を定常分布として持つようなマルコフ連鎖をなすことが知られています.
具体例
具体的な分布を用いて実験してみましょう. まず知りたい分布はガンマ分布とします. 今回は正規化係数がきれいな形をしているので, \(\pi(x)\) がそのまま使えます.
\[ \pi(x) = \mathrm{Gam}(x \mid 2, 2) = xe^{-2x} \]
提案分布は, 直前のサンプルを中心とする正規分布にしてみます.
\[ q(x_* \mid x_t) = \mathcal{N}(x_* \mid x_t, 1.0) \]
すると \(q(x_* \mid x_t) = q(x_t \mid x_*)\) を満たすので, 受理確率は以下のように簡単になります.
\[ \alpha(x_t, x_*) = \min\left\{\frac{\pi(x_*)}{\pi(x_t)}, 1\right\} \]
julia で書けば以下のようになるでしょう.
using Random
# ガンマ分布
gam(x) = x * exp(-2.0 * x)
# 受理確率 (rand() と比較するため, min{-, 1} というふうに考えなくてよい)
α(x_t, x_c) = gam(x_c) / gam(x_t)
function mh(burn_in, iter)
# 初期値
x = 1.0
samples = Vector{Float64}()
for _ = 1:burn_in
x = next_sample(x)
end
for _ = 1:iter
x = next_sample(x)
push!(samples, x)
end
return samples
end
function next_sample(x)
# x を中心とする分散が1であるような正規分布から x_c を取得
x_c = randn() + x
acceptance_rate = α(x, x_c)
if acceptance_rate < rand()
return x
else
return x_c
end
endこれを histogram(mh(10000, 1000), bins = 50) のように実験してみると, 以下のようなヒストグラムが得られました.
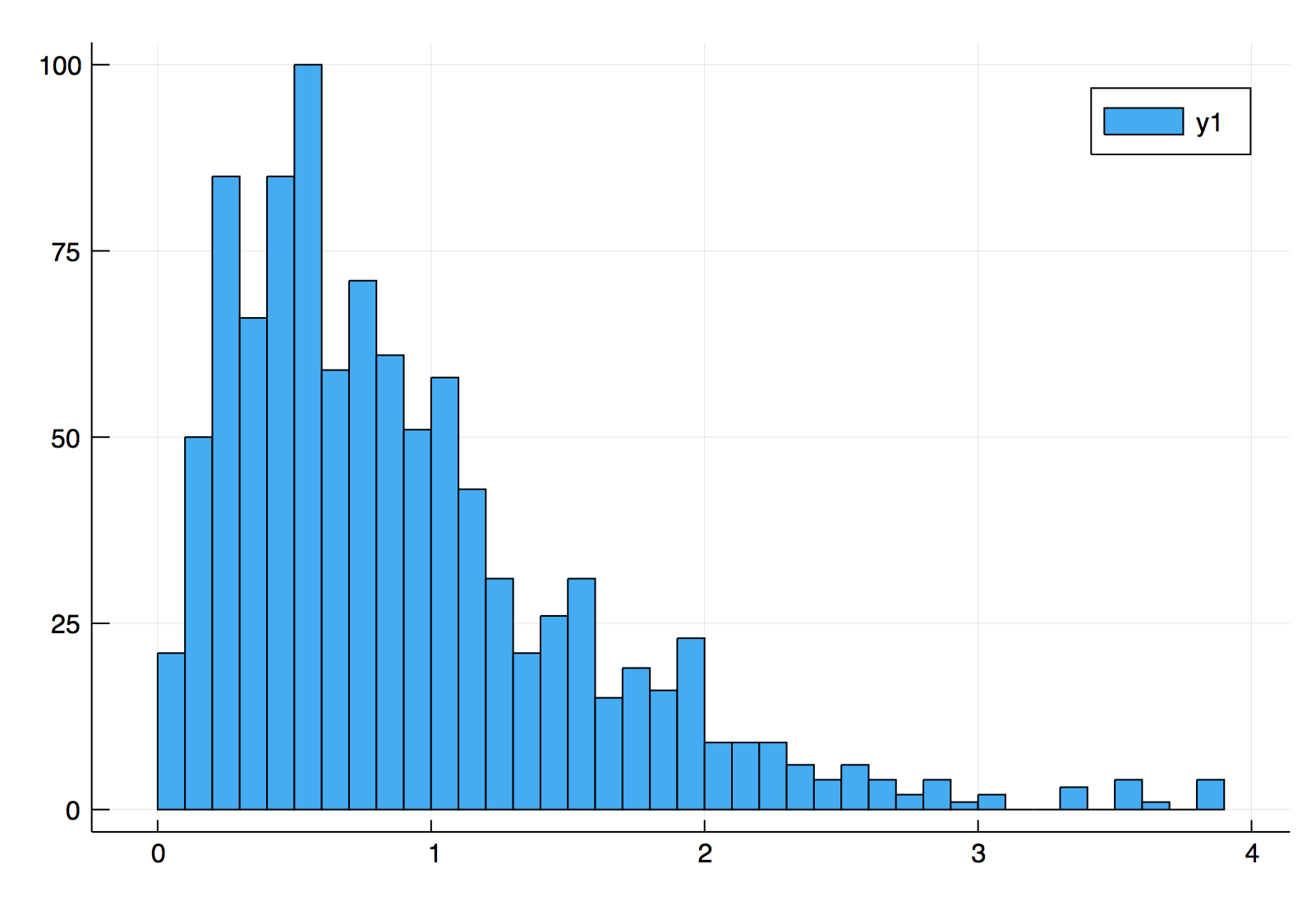
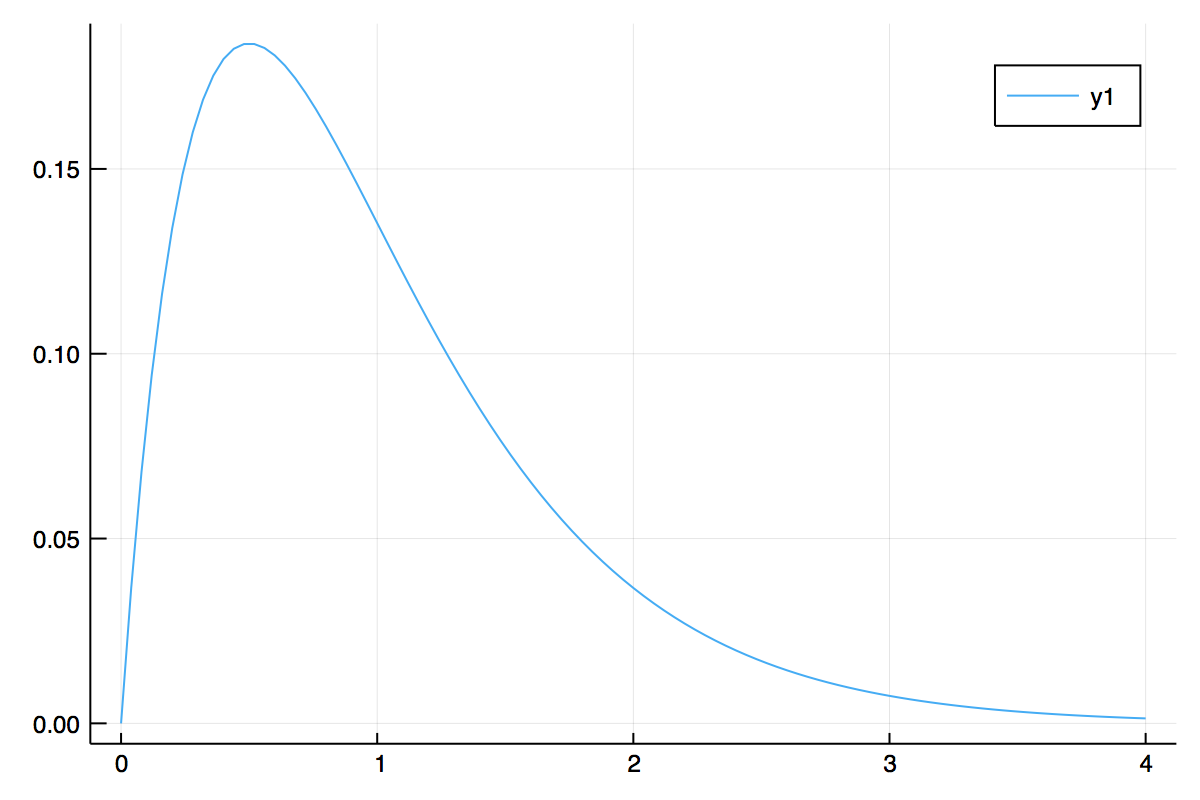
\(\mathrm{Gam}(2, 2)\) の密度関数は次のような形をしていますから, おおかたの形は捉えられていることが分かります.
種類
提案分布の選び方によっては特別に名前がつけられています.
Metropolis Algorithm
\(q(y \mid x) = q(x \mid y)\) が成り立つ場合, Metropolis Algorithm と呼びます.
上のガンマ分布の例がこれに当てはまります. 受理確率が簡単な形をしています.
Random Walk Metropolis Hastings
\(q(y \mid x) = f(y - x)\) と表せる場合, マルコフ連鎖はランダムウォークとなります.
この場合を Random Walk Metropolis Hastings と呼びます. ガンマ分布の例はこれにも当てはまります.
Independent Metropolis Hastings
\(q(y \mid x) = f(y)\) と表せる場合, Independent Metropolis Hastings と呼びます.
課題
理論的には上記のアルゴリズムでサンプリングが可能です. しかしパラメータの数が多いと棄却率が高くなり, かなり多くのサンプルが必要となってしまいます.
提案分布として, 直前のサンプルを中心とした高次元正規分布を採用したとしましょう. この場合は提案分布である正規分布の分散を小さくすれば, 棄却率を下げることができます.
しかしサンプリング1回あたりに進める距離が小さくなるため, 結局多くのサンプルが必要になってしまいます.
成分ごとにMH法
概要
上の問題の原因は, 高次元であることです. 全パラメータが揃って受理されなくてはならないため, パラメータの数が増えるにしたがって受理確率は指数関数的に下がります.
したがってこの問題の解決策として, 成分ごとにサンプリングする方法が考えられます.
アルゴリズム
変数を \(N\) 個持つモデルを考えているとしたら, 以下のようなアルゴリズムになるでしょう.
- \(x_{1, t}, x_{2, t}, \ldots, x_{N, t}\) まで得られたとする.
- 提案分布 \(q_1(x \mid x_{1, t})\) から \(x_{1, t+1}\) の候補 \(x_{1, *}\) を取得.
- 受理確率 \(\alpha_1(x_{1, t}, x_{1, *})\) により 受理/棄却 を決定.
- 中略.
- 提案分布 \(q_k(x \mid x_{k, t})\) から \(x_{k, t+1}\) の候補 \(x_{k, *}\) を取得.
- 受理確率 \(\alpha_k(x_{k, t}, x_{k, *})\) により 受理/棄却 を決定.
- これを \(N\) まで行う.
- これを繰り返す.
ただし受理確率は以下の通りです.
\[ \alpha_k(x_{k, t}, x_{k, *}) = \min\left\{ \frac{ \pi(x_{k, *} \mid x_{1, t+1}, \ldots, x_{k-1, t+1}, x_{k+1, t}, \ldots, x_{N, t})q_k(x_{k, t} \mid x_{k, *}) }{ \pi(x_{k, t} \mid x_{1, t+1}, \ldots, x_{k-1, t+1}, x_{k+1, t}, \ldots, x_{N, t})q_k(x_{k, *} \mid x_{k, t}) }, 1 \right\} \]
しかし全ての成分を個別に扱うことで, 実行時間が非現実的なほどまで増大することもありえます. そのような場合は変数をグルーピングし, そのグループごとにサンプリングするという工夫も考えられるでしょう.
ギブスサンプリングとの違い
ギブスサンプリングは成分ごとのMH法の1種です. ギブスサンプリングは, 条件付き分布 \(\pi(x_k \mid x_1, \ldots, x_{k-1}, x_{k+1}, \ldots x_{N})\) が既知(直接サンプリング可能であるということ)である場合に適用できるアルゴリズムですね.
この場合はわざわざよそから提案分布をもってくる必要がありません. この条件付き分布からサンプルすればいいからです.
すると受理確率は常に \(1\) となり, 棄却されることのないMH法となります.
早期リジェクトで高速化
概要
高次元の呪いを解くためには成分ごとにサンプリングすればいいと述べました. しかしそれでは実行時間が大幅に増加してしまいます.
変数をグループ化し, グループごとにサンプリングするという方法も考えられますが, それだけではなかなか計算量をへらすことができません.
ここでは以下の論文で紹介されている高速化の手法を紹介します.
その手法とは, delayed acceptance と呼ばれるものです. 個人的には早期リジェクトと言ったほうがしっくりくるので, 本記事内ではこう呼ぶことにします.
どうせ棄却(リジェクト)されるなら早いほうがいい, というのがこの手法のアイデアです.
アルゴリズム
では具体的に説明していきます. 記号が複雑になるので, 変数をまるごとサンプリングする場合を考えます(もしくは1変数の場合を考えていると思っていただいても構いません).
さて, もともとのアルゴリズムにおける受理確率は
\[ \alpha(x_t, x_*) = \min\left\{\frac{\pi(x_*)q(x_t \mid x_*)}{\pi(x_t)q(x_* \mid x_t)}, 1\right\} \]
でした. 確率の概念に当てはめるために \(1\) と比較しているだけなので, 本質的に重要なのは分数の部分です. ここが以下のように積に分解できたとしましょう.
\[ \frac{\pi(x_*)q(x_t \mid x_*)}{\pi(x_t)q(x_* \mid x_t)} = \prod_{i = 1}^d \rho_i(x_t, x_*) \]
たとえば \(0.72 = 0.8 \times 0.9\) のような分解です. この分解は以下の2つが等価であることを表しています.
- \(0.72\) の確率で1つのハードルを超える.
- \(0.8\) の確率で1つめのハードルを超え, \(0.9\) の確率で2つめのハードルを超える.
裏を返せば, １つめのハードルが超えられない時点で2つめは飛ぶ必要がないということです. これにより早期リジェクトが実現します.
計算量が少なく受理確率が低いものをひとつめのハードルとして据えられたら, リジェクトの効率が高くなり, 結果としてサンプリングの高速化が望めます.
ここで注意しておきたいのが, 決して受理される場合の計算量を減らすことにはならないということです. あくまで効率化されるのは棄却のみです.
ベイズ推論においては知りたい分布である事後分布が \(p(D \mid x)p(x)\) のように2つの積になっています. 提案分布が対称である Metropolis Algorithm を利用すれば, 受理確率は次のような積に分解できます.
\[ \frac{p(D \mid x_*)}{p(D \mid x_t)} \cdot \frac{p(x_*)}{p(x_t)} \]
もし事前分布の計算量が多いなら, まずは尤度関数のほうで 受理/棄却 を判定することで, 全体的な実行時間の削減が望めます.