カイ二乗検定にイェーツ補正は必要か？

ラプラスの定理

母比率に関する検定を行う場合、多くの場合 z 検定やカイ二乗検定を使います。標本は二項分布に従うのに、正規分布やカイ二乗分布のような連続分布を使うことができるのは、次のようなラプラスの定理があるからです。

二項分布 $\mathrm{Bi}(n, p)$ は、 $n$ が大きいとき正規分布 $\mathrm{N}(np, np(1-p))$ に近づく。

イェーツ補正

いくら近似できるといっても、片や離散分布で片や連続分布ですから、少なからずズレが生じます。それを補正するのがイェーツ補正です。イェーツの連続性補正や半整数補正などとも呼ばれます。

例として二項分布 $\mathrm{Bi}(10, 0.5)$ を考えます。ラプラスの定理から、これは正規分布 $\mathrm{N}(5, 2.5)$ に近似できます。どれほど近似できているかは分布をまとめて図示するとよくわかります。

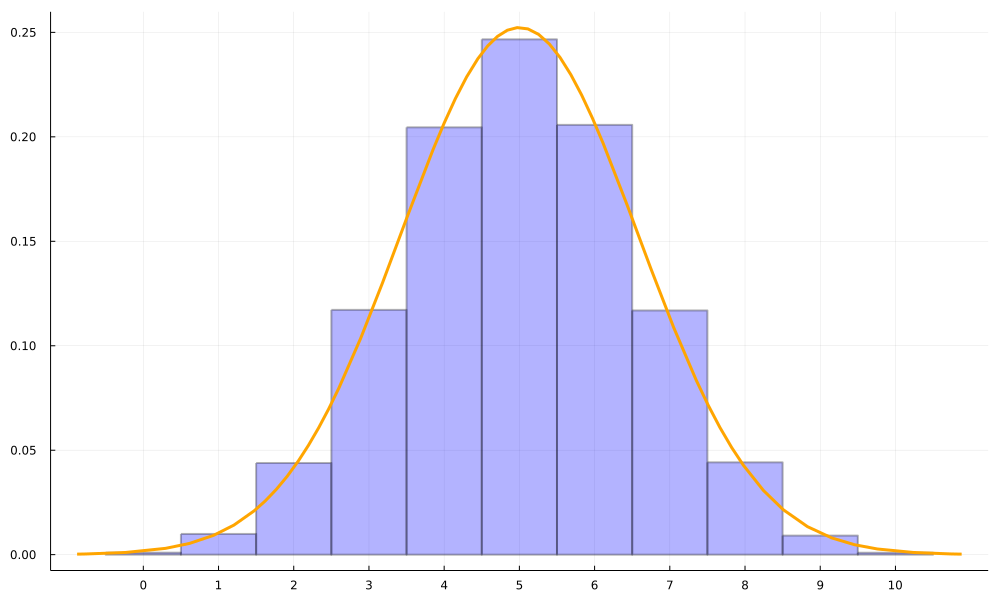
ここで、二項分布 $\mathrm{Bi}(10, 0.5)$ に従う確率変数を $X$ とし、正規分布 $\mathrm{N}(5, 2.5)$ に従う確率変数を $Z$ とします。二項分布を正規分布で近似できるというのは、 $P(a \leq X \leq b)$ を $P(a \leq Z \leq b)$ に置き換えられることと同等です。

例として $P(3 \leq X \leq 6)$ を考えてみます。これは下の図の紫の領域の面積です。図をよく見ると、 $P(3 \leq Z \leq 6)$ よりも $P(2.5 \leq Z \leq 6.5)$ のほうがよく近似できていますよね。このように、上下ともに 0.5 ずつ補正して確率計算することを、イェーツ補正と言います。

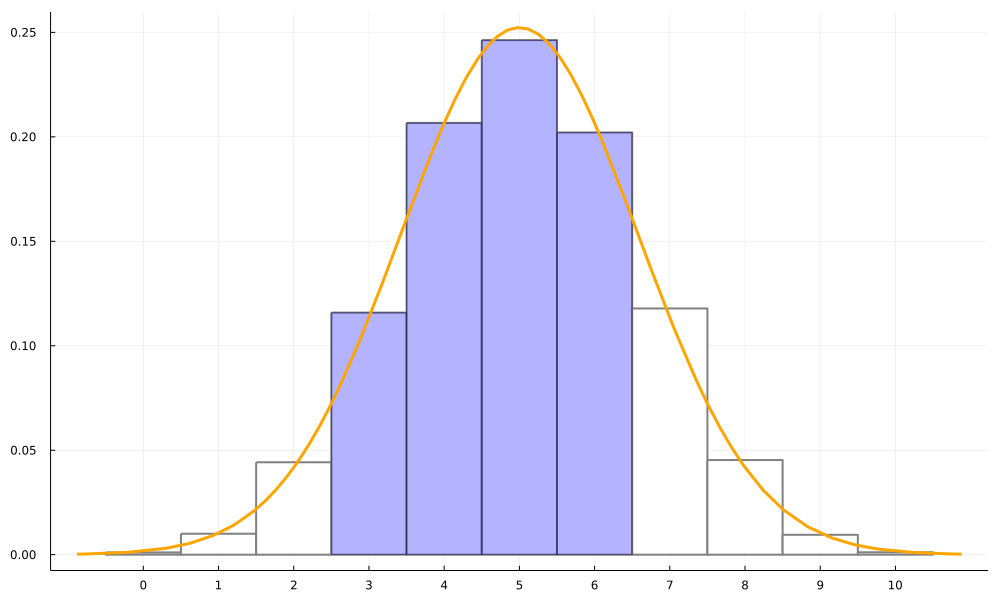
イェーツ補正は必要か

統計学の本を見ると、サンプルサイズが小さい場合はイェーツ補正を行うよう書かれています。それと同時に、具体的な参照先は省略しますが、イェーツ補正はすべきでないとの意見も見られます。

本当にイェーツ補正をすべきなのかを改めて考えてみます。

上では図の見やすさの関係から、 $\mathrm{Bi}(10, 0.5)$ を考えていましたが、ここでは $\mathrm{Bi}(100, 0.5)$ を考えることにします。

確率の観点から

ためしに Julia で次の 3 つの確率値を計算してみました。

$P(40 \leq X \leq 50)$
$P(40 \leq Z \leq 50)$
$P(39.5 \leq Z \leq 50.5)$

計算結果はコードコメントに書きましたが、やはりイェーツ補正をしたほうがより良い近似値が得られそうですね。

using Distributions
using Random

b = Binomial(100, 0.5)

# 第二引数は標準偏差であることに注意
n = Normal(50, 10 * 0.5)

# P(40 ≦ X ≦ 50) = 0.52219
@info cdf(b, 50) - cdf(b, 39)

# P (40 ≦ Z ≦ 50) = 0.47724
@info cdf(n, 50) - cdf(n, 40)

# P (39.5 ≦ Z ≦ 50.5) = 0.52196
@info cdf(n, 50.5) - cdf(n, 39.5)

有意水準の観点から

コインの表の出る確率が 0.5 かどうかを、検定を使って調べたいとします。検定の設定は以下の通りです。

帰無仮説: コインの表の出る確率は 0.5 である
有意水準: 0.05
両側検定
サンプルサイズ: 100

帰無仮説が棄却されるかを判断するには p 値を計算しなくてはならないわけですが、次の 3 通りの方法を考えます。具体例を併記していますが、両側検定なので 2 倍していることに注意です。

二項分布から計算される p 値
- 近似していないので正しい p 値ということになる
- 表が 40 回出た場合は $2 \cdot P(X \leq 40)$
近似された正規分布から計算される p 値
- 表が 40 回出た場合は $2 \cdot P(Z \leq 40)$
近似された正規分布からイェーツ補正を施して計算される p 値
- 表が 40 回出た場合は $2 \cdot P(Z \leq 40.5)$

この設定のもとで α エラーが発生する確率をシミュレーションを通して計算します。シミュレーション用 Julia コードは記事の最後に載せ、ここでは結果だけ示します。

確率的な要素があるので実行ごと結果は違うのですが、今手元で実行した結果は以下のようになりました。

p 値の計算方法	α エラーが発生した回数
二項分布	338
近似された正規分布	532
近似された正規分布 + イェーツ補正	338

有意水準を 5% に設定したということは、α エラーが発生する確率を 5% に設定したということに他なりません。上の表を見ると、イェーツ補正をして p 値を計算した場合、α エラーが発生したのは 10000 回の施行のうち 338 回でした。これではまるで有意水準を 3.38% に設定したかのようですね。

一方イェーツ補正を行わずに p 値を計算した場合、α エラーが発生したのは 532 回でした。こちらのほうが有意水準の 5% に近いですね。

まとめ

以上の結果を受けて、個人的には以下のような使い分けをすることにしました。

単に確率の近似値が欲しい場合は補正する
検定したい場合は補正しない

付録 : Julia コード

p 値計算のシミュレーション

using Distributions
using Random

b = Binomial(100, 0.5)
n = Normal(50, 5)

# 二項分布から計算した正しい p 値
function true_p(x)
    if x == 50
        1.0
    else
        2 * cdf(b, 50 - abs(50 - x))
    end
end

# 近似した正規分布から計算した p 値
function normal_p(x)
    2 * cdf(n, 50 - abs(50 - x))
end

# イェーツ補正した p 値
function corrected_p(x)
    if x == 50
        1.0
    else
        2 * cdf(n, 50.5 - abs(50 - x))
    end
end

samples = rand(b, 10000)

true_ps = map(true_p, samples)
@info length(filter(x -> x <= 0.05, true_ps))

normal_ps = map(normal_p, samples)
@info length(filter(x -> x <= 0.05, normal_ps))

corrected_ps = map(corrected_p, samples)
@info length(filter(x -> x <= 0.05, corrected_ps))

2 枚目のグラフ

using Distributions
using Random
using StatsBase
using StatsPlots

gr(size=(1000, 600))

samples = rand(Binomial(10, 0.5), 10 ^ 5)
h = fit(Histogram, samples, 0:11)
values = h.weights ./ 10 ^ 5

bar(0:10, values, xticks=0:10, color=:white, bar_width=1, linewidth=2, linecolor=:gray, legend=nothing)
bar!(3:6, values[4:7], color=:blue, alpha=0.3, bar_width=1)
p = plot!(Normal(5, sqrt(10) * 0.5), color=:orange, linewidth=3)

savefig(p, "chart.png")