概要
Julia で GLM と Julia で GLMM の続編です。引き続き データ解析のための統計モデリング入門 (通称緑本) に沿ってやっていきます。
理論的背景の解説が主目的でないので、説明なしで専門用語を使うことがあります。
準備
Stan
MCMC ソフトウェアとして Stan を使います。
cmdstan は wiki にある通りにインストールします。
# 適当なディレクトリに clone
$ cd ~/stan
$ git clone https://github.com/stan-dev/cmdstan.git --recursive
$ cd cmdstan
# make コマンドでビルド
$ meke build -j4
# 環境変数を設定
$ export JULIA_CMDSTAN_HOME=$HOME/stan/cmdstan
Julia
Julia から Stan を扱うにはいくつかのパッケージを使います。
- StanSample
- MCMCChains
コード例は Stan.jl にまとまっているので参考にすると良いでしょう。
Bayesian GLM
GLM や GLMM は探索的にコードを実行してたので REPL で事足りましたが、ベイズモデリングはまとまったコードが必要となるため、ファイルに書くことにします。
データは引き続き badhealth を使うことにします。Julia で GLM の記事で以下のようにモデリングしましたが、これをベイズ化します。
glm(@formula(NumVisit ~ Age + BadH), badhealthData, Poisson(), LogLink())
単純に回帰係数に事前分布を与えるだけです。とはいっても stan コード上では明示的に事前分布を書かず、improper prior を使うことにします。
data {
int<lower=1> N;
array[N] int<lower=1> Age;
array[N] int<lower=0, upper=1> BadH;
array[N] int<lower=0> NumVisit;
}
parameters {
real alpha;
real beta1;
real beta2;
}
model {
for (n in 1:N) {
NumVisit[n] ~ poisson(exp(alpha + beta1 * Age[n] + beta2 * BadH[n]));
}
}
モデリングに必要なコードを関数にまとめたのが以下です。GLMM のベイズ化でも使い回します。
# hierarchical_bayes.jl
using StanSample, MCMCChains, RDatasets, StatsPlots, DataFrames, CategoricalArrays
function load_data()
df = dataset("COUNT", "badhealth")
data = Dict(pairs(eachcol(df)))
data = merge(data, Dict(:N => length(data[:NumVisit])))
return df, data
end
function read_stan_model(filename::String)
f = open(filename, "r")
model = read(f, String)
close(f)
return SampleModel(filename, model)
end
function mcmc(
sample_model::SampleModel, data::Dict, num_warmups::Int, num_samples::Int, save_warmup::Bool;
num_chains::Int=4
)
stan_sample(
sample_model,
data=data,
num_chains=num_chains,
num_warmups=num_warmups,
num_samples=num_samples,
save_warmup=save_warmup
)
return read_samples(sample_model, :mcmcchains)
end
function plot_glm_prediction(df::DataFrame, chns::Chains)
# ひとつめの chain のサンプルだけを取り出し Matrix に変換
# append_chains を false にすることで、chain をひとまとめにしないようにしてくれる
samples = Array(chns, append_chains=false)[1]
goodHlines = map(eachrow(samples)) do coefs
x -> exp([1, x, 0]' * coefs)
end
badHlines = map(eachrow(samples)) do coefs
x -> exp([1, x, 1]' * coefs)
end
plot(
df.Age,
df.NumVisit,
group=df.BadH,
t=:scatter,
xaxis="Age",
yaxis="NumVisit",
legend=nothing,
)
plot!(goodHlines, color=:blue, alpha=0.05)
plot!(badHlines, color=:red, alpha=0.05)
end
function plot_glmm_prediction(df::DataFrame, chns::Chains)
samples = Array(chns, append_chains=false)[1]
# ランダム効果 r のサンプルを取り除く
samples = samples[:, [1, 2, 3, end]]
goodHlines = map(eachrow(samples)) do coefs
x -> exp([1, x, 0, 1]' * coefs)
end
badHlines = map(eachrow(samples)) do coefs
x -> exp([1, x, 1, 1]' * coefs)
end
plot(
df.Age,
df.NumVisit,
group=df.BadH,
t=:scatter,
xaxis="Age",
yaxis="NumVisit",
legend=nothing,
)
plot!(goodHlines, color=:blue, alpha=0.05)
plot!(badHlines, color=:red, alpha=0.05)
end
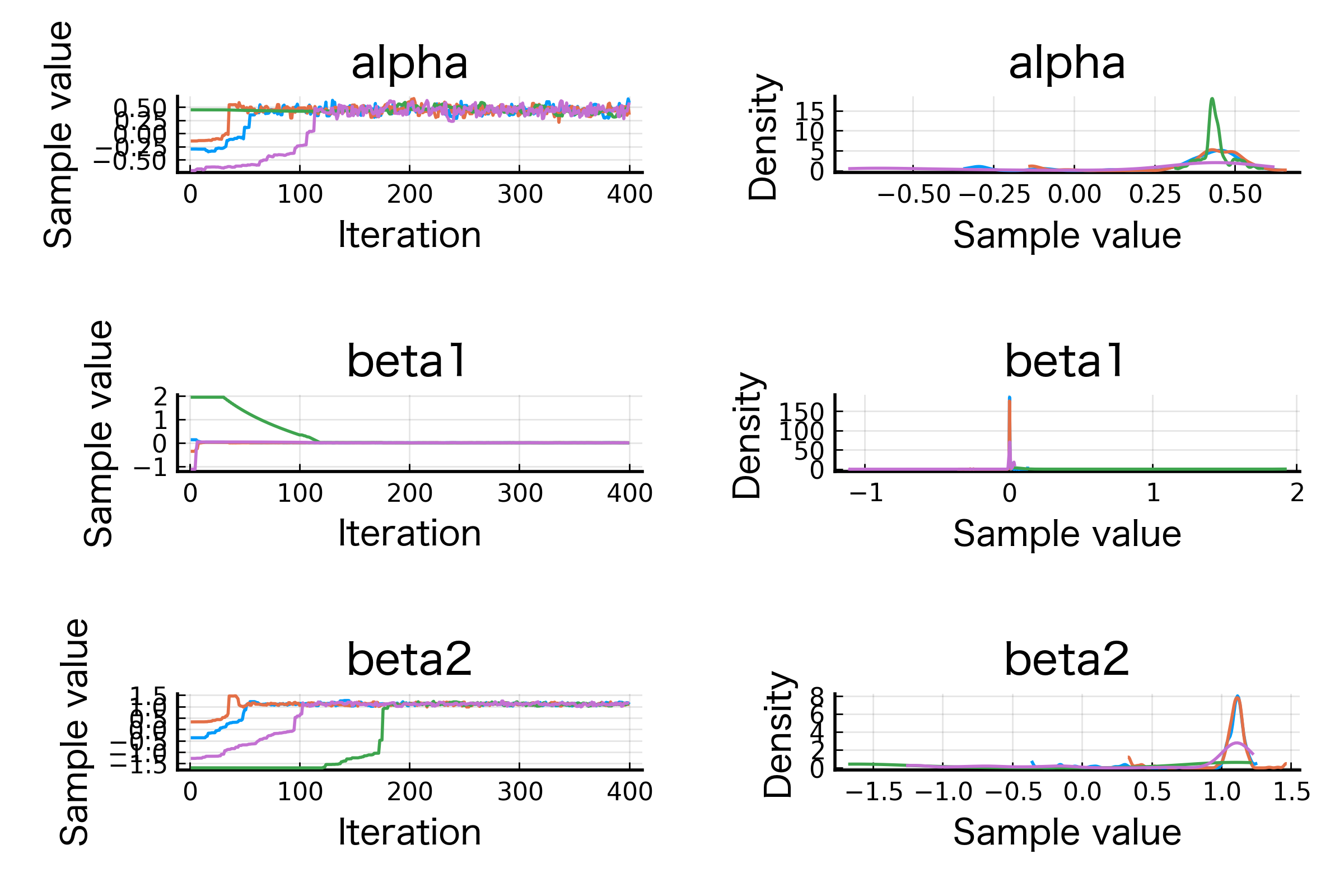
最後の plot 関数により以下のような画像が出力されるはずです。初期値にもよるでしょうが、少なくとも 200 サンプル以降では定常分布に収束してそうですね。
定常分布からのサンプルは数百から数千は必要でしょうが、ここでは図示に使いたいので 100 だけにしてみます。事後分布からの 100 個のサンプルから回帰曲線 (exp にかませているので曲線) を 100 本生成し、図示してみます。それが plot_glm_prediction 関数です。散布図も一緒にプロットしています。
julia> chns = mcmc(sm, data, 200, 100, false)
julia> plot_glm_prediction(df, chns)
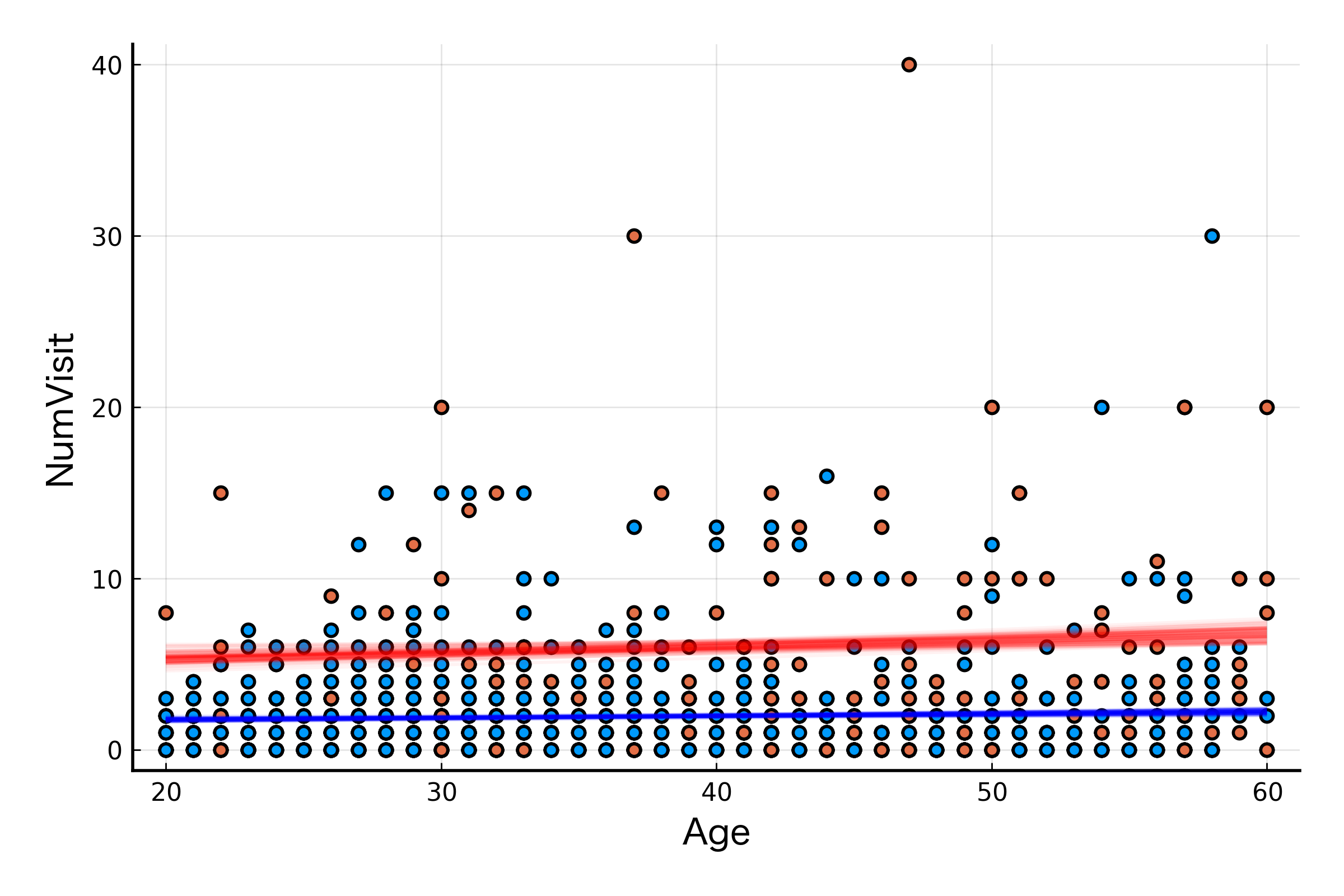
すると以下のような画像が得られます。事後分布の分散がとても小さいため、ほとんど 1 本の曲線かのように寄り集まっています。
Bayesian GLMM
続いて GLMM をベイズ化していきます。前回の記事 では個人差をモデルに組み込むために以下のように GLMM によりモデリングをしました。
data.Id = categorical(1:(length(data.NumVisit)))
model = fit(MixedModel, @formula(NumVisit ~ Age + BadH + (1|Id)), data, Poisson(), LogLink())
ランダム効果である個人差は平均 0 の正規分布に従うとしています。今回は分散パラメータに事前分布を与えることで階層ベイズモデルにします。stan コードは以下です。
# glmm.stan
data {
int<lower=1> N;
array[N] int<lower=1> Age;
array[N] int<lower=0, upper=1> BadH;
array[N] int<lower=0> NumVisit;
}
parameters {
real alpha;
real beta1;
real beta2;
vector[N] r;
real<lower=0> s;
}
model {
s ~ gamma(2, 0.1);
for (n in 1:N) {
r[n] ~ normal(0, s);
NumVisit[n] ~ poisson(exp(alpha + beta1 * Age[n] + beta2 * BadH[n] + r[n]));
}
}
s の事前分布にガンマ分布を設定していますが、ガンマ分布のパラメータについては こちら を参考に設定しました。いろいろ変えて試すなら、外から渡すようにしたほうが良いかもしれませんね。
まずは先ほどと同じように、warmup も含めて収束の様子を見てみましょう。chns の中にはランダム効果のサンプルも含まれているため、plot 関数には図示したいパラメータだけを渡すようにしてください。
julia> sm = read_stan_model("glmm.stan");
julia> chns = mcmc(sm, data, 200, 200, true);
julia> plot(chns, [:alpha, :beta1, :beta2, :s])
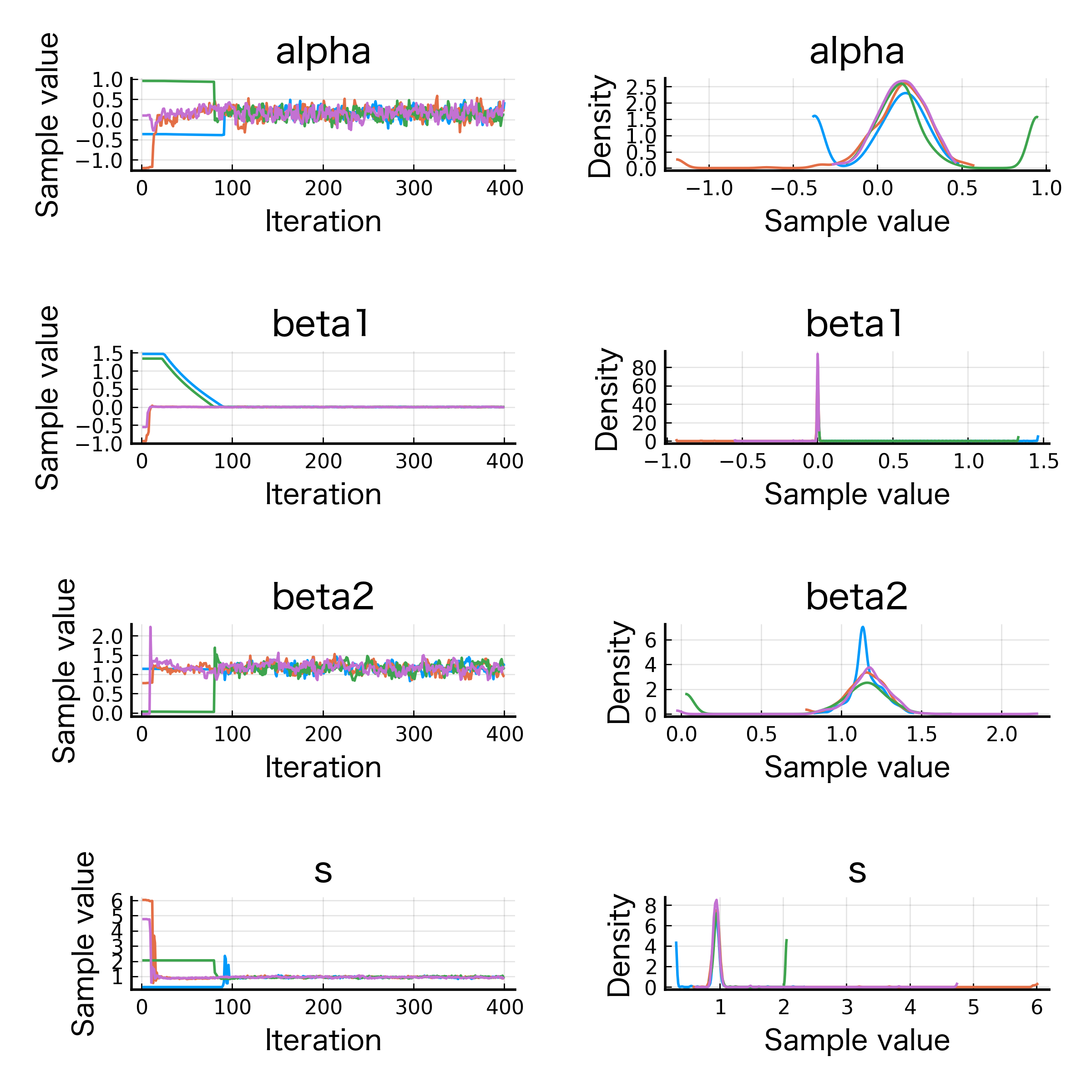
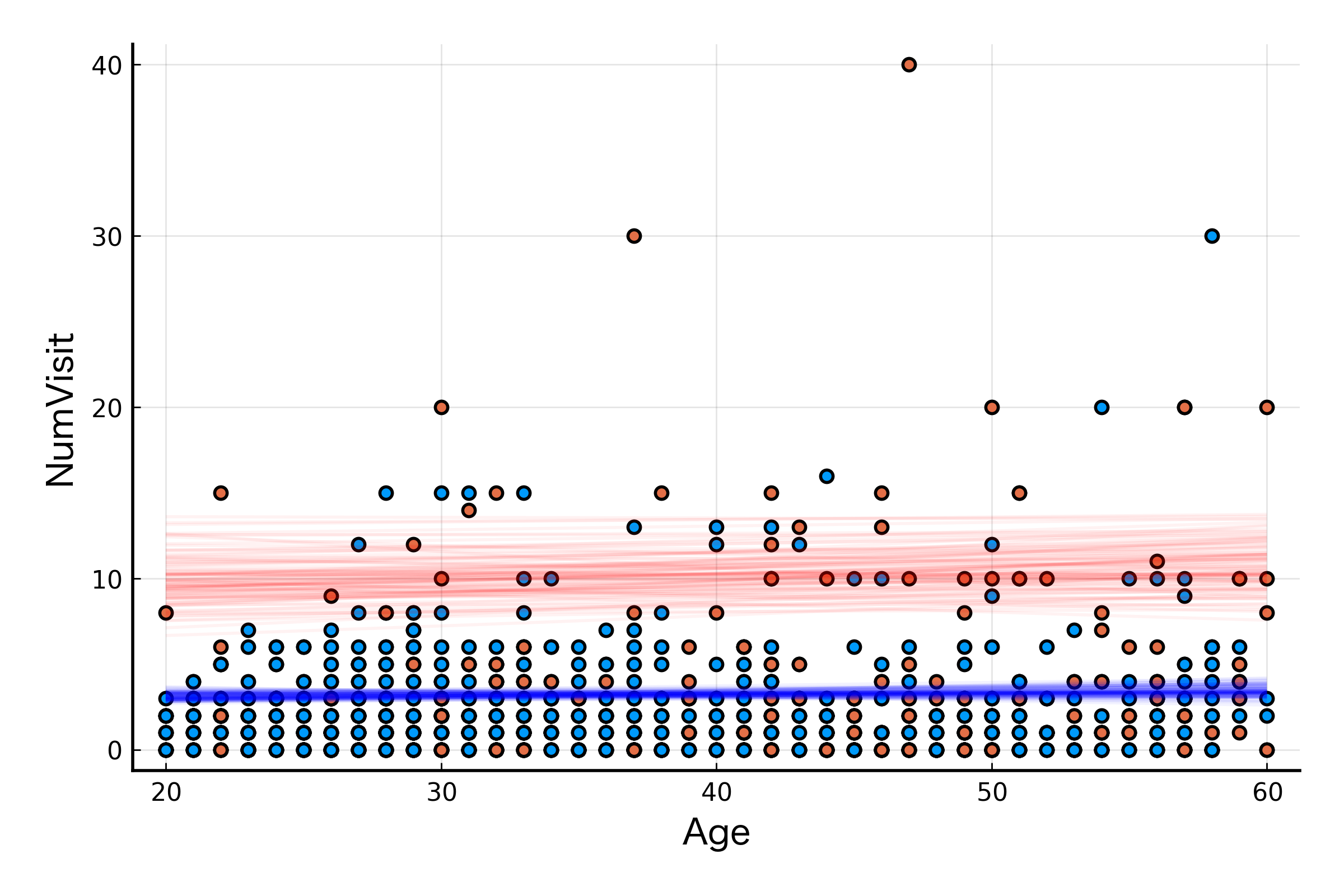
GLM のときと同じように warmup は 200 サンプルくらいあれば十分そうですね。こちらも回帰曲線群を図示してみます。
julia> chns = mcmc(sm, data, 200, 100, false);
julia> plot_glmm_prediction(df, chns)
さいごに
GLM と GLMM をそれぞれベイズ化するための一連のコードを見てきました。単に本を読むだけではなく実際に手を動かすことでより理解が深まったように思います。今後は社内にあるデータで遊んでみようと思います。