Julia で GLM の続編です。
概要
Julia で GLM では、badhealth データを用いて可視化、GLM モデリング、AIC によるモデル選択をやりました。
本記事ではその続きとして、GLMM に発展させることを考えます。参考文献は引き続き データ解析のための統計モデリング入門 (通称緑本) です。
また本記事は GLMM を解説することが目的ではないため、説明なしで専門用語を使うことがあります。
準備
前回の記事 で導入したパッケージ以外に新たに必要なのは MixedModels パッケージです。REPL を起動し、パッケージ群とデータセットを読み込んでおきます。
julia> using CategoricalArrays, DataFrames, Distributions, GLM, MixedModels, Plots, RDatasets, Statistics, StatsModels, StatsPlots
julia> data = dataset("COUNT", "badhealth")
過分散
まずは GLMM に発展させるモチベーションから確認していきます。badhealth は以下のような 3 つのカラムからなるデータでした (詳しくはこちら)。
- NumVisit (整数): 病院への通院回数
- Age (整数): 年齢
- BadH (0 or 1): 健康状態
前回の記事では、BadH と Age を回帰変数に含めた Poisson 回帰を考えました。それはつまり以下のような仮定に基づいてモデリングしていることに等しいです。
- Age = 20 かつ BadH = 0 のデータに限定すると NumVisit は Poisson 分布に従う
- Age = 20 かつ BadH = 1 のデータに限定すると NumVisit は Poisson 分布に従う
- Age = 21 かつ BadH = 0 のデータに限定すると NumVisit は Poisson 分布に従う
- ...
この仮定が妥当かどうか、Age = 28 かつ BadH = 0 のデータを見てみましょう。もし Poisson 分布に従っているなら平均と分散は等しくなるはずですが、そうはなっておらず、分散が平均の 3 倍以上になっています。この状態を過分散と言います。
julia> data28good = filter(row -> row.Age == 28 && row.BadH == 0, data)
julia> mean(data28good.NumVisit)
2.056603773584906
julia> var(data28good.NumVisit)
6.631349782293177
前回やった GLM によるモデリングがどれほどデータにフィットしているかを図示して確かめてみます。対数リンク関数を使っているため、線形予測子を exp に適用するのを忘れないよう注意です。
julia> glmModel = glm(@formula(NumVisit ~ Age + BadH), data, Poisson(), LogLink())
julia> histogram(data28good.NumVisit, norm=true, bins=-0.5:1:(maximum(data28good.NumVisit) + 0.5))
julia> plot!(Poisson(exp([1, 28, 0]' * coef(glmModel))), t=:line, lw=2)
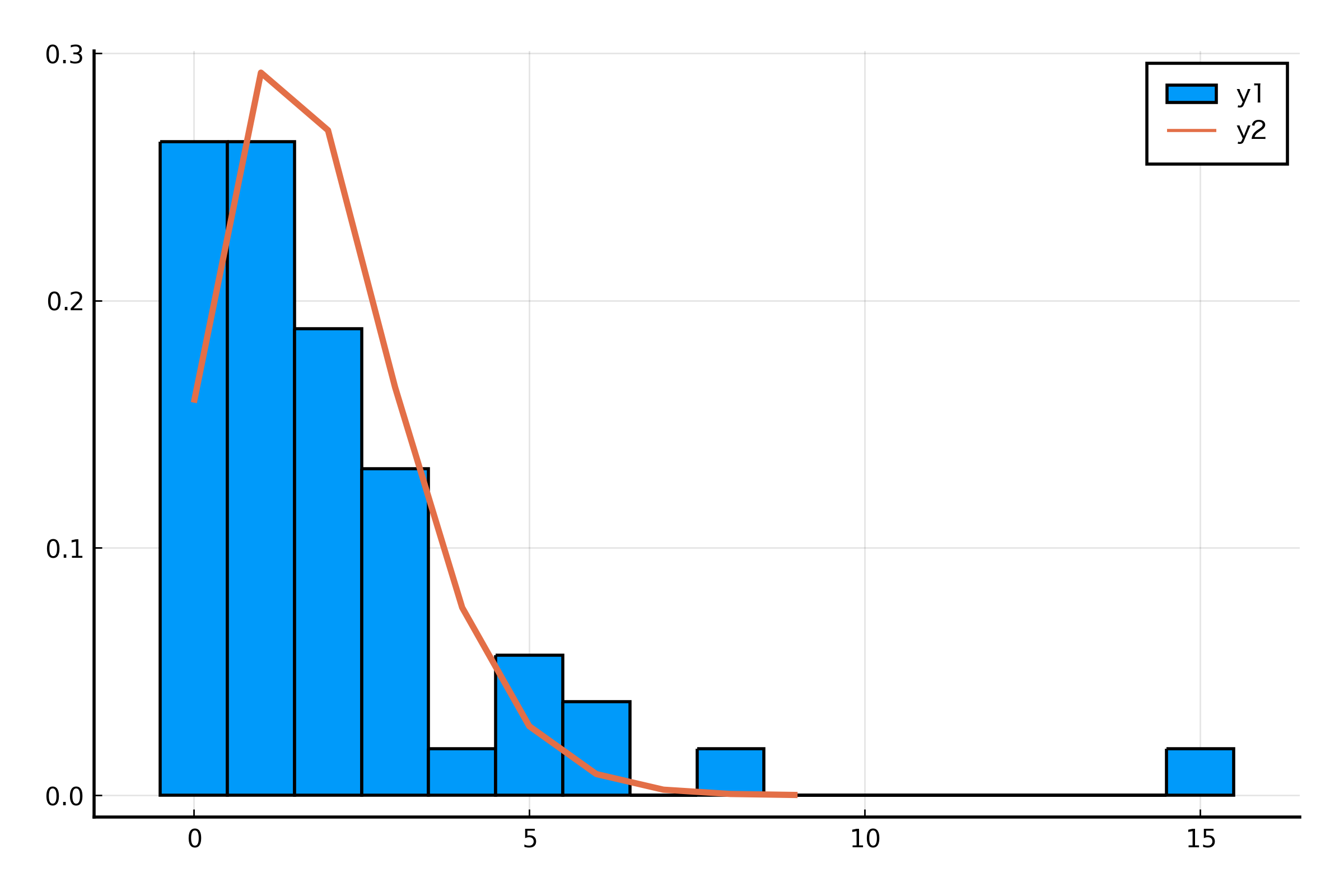
データの分散が大きいためか、Poisson 分布へのあてはめがうまくいってなさそうな感じがしますね。
このような過分散なデータに使える GLMM をこれから見ていきます。
GLMM
上で見たように、Age と BadH で細分化しただけではデータは過分散なのでした。もし他に収入状況を示す Income のような観測値があるのなら、それをモデルに含めることで過分散が解消されるかもしれません。
しかしこのデータセットには Age と BadH しかないため、GLMM を利用して「未観測データによる変動」を表現する必要があります。
ひとまず緑本と同じように未観測の個人差があると仮定してみます。これは以下のようにモデリングしていることに等しいです。
Julia コードは以下の通りです。個人ごとにランダム効果が発生していると考えたいので、データに通し番号をつけた上でモデリングします。
julia> data.Id = categorical(1:length(data.NumVisit))
julia> model = fit(MixedModel, @formula(NumVisit ~ Age + BadH + (1|Id)), data, Poisson(), LogLink())
Minimizing 119 Time: 0:00:00 ( 3.63 ms/it)
Generalized Linear Mixed Model fit by maximum likelihood (nAGQ = 1)
NumVisit ~ 1 + Age + BadH + (1 | Id)
Distribution: Poisson{Float64}
Link: LogLink()
logLik deviance AIC AICc BIC
-2227.6815 2288.1128 4463.3629 4463.3986 4483.4722
Variance components:
Column Variance Std.Dev.
Id (Intercept) 0.865232 0.930179
Number of obs: 1127; levels of grouping factors: 1127
Fixed-effects parameters:
────────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
────────────────────────────────────────────────────
(Intercept) 0.146076 0.133282 1.10 0.2731
Age 0.00205309 0.00347403 0.59 0.5545
BadH 1.16767 0.110826 10.54 <1e-25
────────────────────────────────────────────────────
さて、GLMM では目的変数とランダム効果の 2 つの分布が登場しますが、NumVisit だけの分布は次のようにランダム効果 を積分消去すれば得られます。GLM では Age と BadH で細分化したデータの NumVisit が Poisson 分布に従うという仮定をしていましたが、GLMM では Poisson 分布を正規分布で混ぜ合わせたものになっています。
GLM ではうまいことあてはめができていませんでしたが、GLMM ではどうなっているでしょうか。図示して確かめてみたいところです。混合分布の図示は乱数を発生させることで行います。
julia> sigma = model.σs[:Id][1]
julia> N = 100000
julia> samples = rand(Normal(0, sigma), N)
julia> samples = map(s -> rand(Poisson(exp([1, 28, 0]' * fixef(model) + s))), samples)
julia> histogram(data28good.NumVisit, norm=true, bins=-0.5:1:(maximum(data28good.NumVisit) + 0.5))
julia> plot!(0:15, fit(Histogram, samples, 0:16).weights ./ N, t=:line, lw=2)
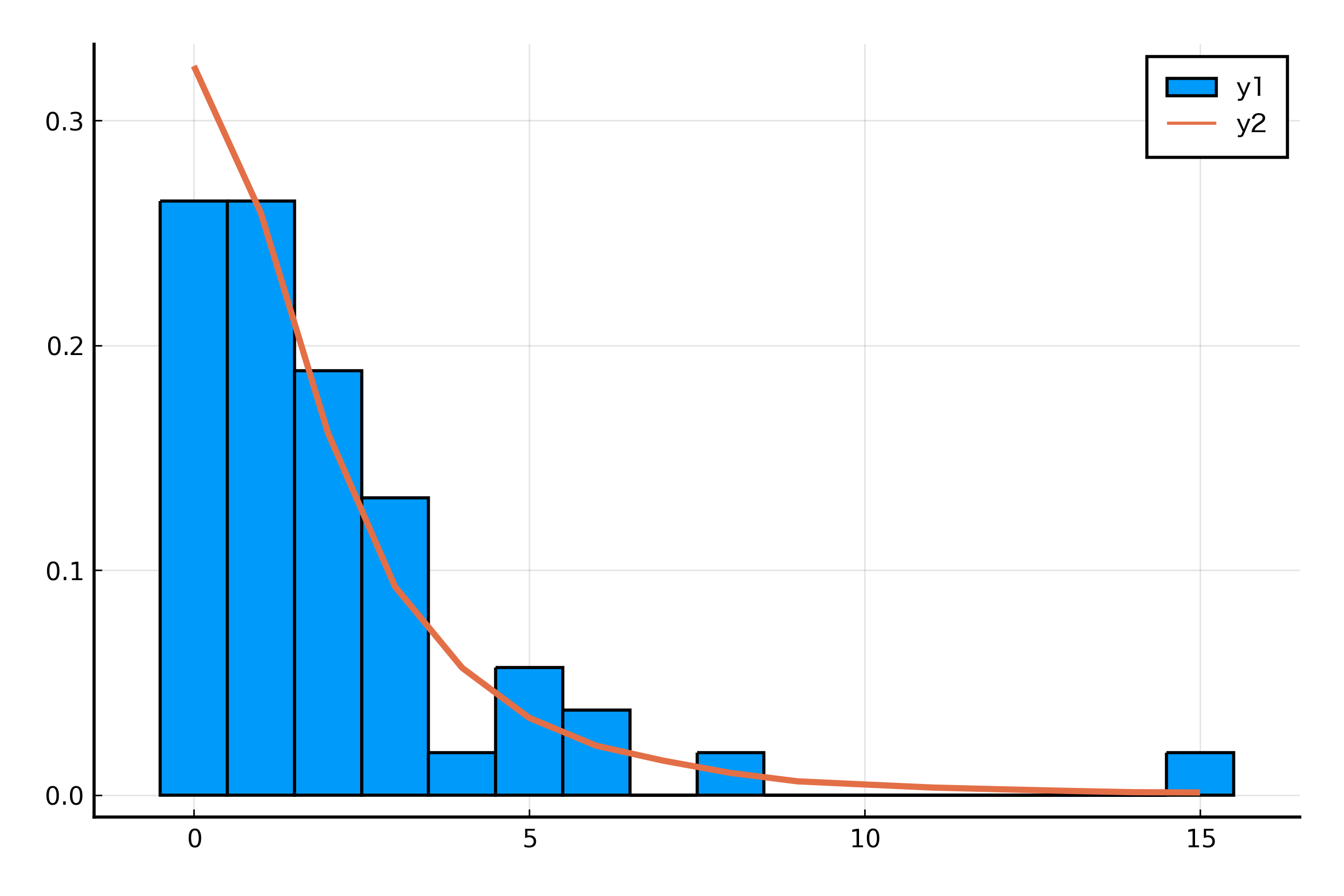
GLM よりもあてはめがうまくいってそうな感じがしないでもないです。一応混合分布の分散も計算しておきましょう。
julia> mean(data28good.NumVisit), var(data28good.NumVisit)
(2.056603773584906, 6.631349782293177)
julia> mean(samples), var(samples)
(1.8523, 6.449329642964297)
単一の Poisson 分布では表現できなかった過分散性が再現できていますね。
疑問
GLM と GLMM をやってきてひとつ疑問が浮かびました。カテゴリカルな観測値が存在する場合、それを GLM の説明変数として使うのと、GLMM のランダム効果のグルーピングとして使うのと、どちらが良いのでしょうか?つまり以下の 2 つのモデリングを比較してどちらが良いか、ということです。
# y が目的変数で x がカテゴリカル変数
model1 = glm(@formula(y ~ x), data)
model2 = fit(MixedModel, @formula(y ~ (1|x)), data)
badhealth データを使って調べてみます。
julia> data.BadH = categorical(data.BadH);
julia> model1 = glm(@formula(NumVisit ~ BadH), data, Poisson(), LogLink())
StatsModels.TableRegressionModel{GeneralizedLinearModel{GLM.GlmResp{Vector{Float64}, Poisson{Float64}, LogLink}, G
LM.DensePredChol{Float64, LinearAlgebra.Cholesky{Float64, Matrix{Float64}}}}, Matrix{Float64}}
NumVisit ~ 1 + BadH
Coefficients:
────────────────────────────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|) Lower 95% Upper 95%
────────────────────────────────────────────────────────────────────────
(Intercept) 0.661621 0.0225466 29.34 <1e-99 0.61743 0.705812
BadH: 1 1.1493 0.0443643 25.91 <1e-99 1.06235 1.23625
────────────────────────────────────────────────────────────────────────
julia> model2 = fit(MixedModel, @formula(NumVisit ~ (1|BadH)), data, Poisson(), LogLink())
Generalized Linear Mixed Model fit by maximum likelihood (nAGQ = 1)
NumVisit ~ 1 + (1 | BadH)
Distribution: Poisson{Float64}
Link: LogLink()
logLik deviance AIC AICc BIC
-2828.3077 3489.3653 5660.6154 5660.6261 5670.6700
Variance components:
Column VarianceStd.Dev.
BadH (Intercept) 0.32896 0.57355
Number of obs: 1127; levels of grouping factors: 2
Fixed-effects parameters:
────────────────────────────────────────────────
Coef. Std. Error z Pr(>|z|)
────────────────────────────────────────────────
(Intercept) 1.23494 0.406168 3.04 0.0024
────────────────────────────────────────────────
GLM も GLMM も以下の 2 つの仮定を置いていることに違いはありません。
- BadH = 0 に限定したデータは Poisson 分布に従う
- BadH = 1 に限定したデータは Poisson 分布に従う
では GLM と GLMM のそれぞれで推定された Poisson 分布の平均パラメータを比較してみます。
GLMM のランダム効果の推定値は ranef 関数を使えばわかります。第一成分が BadH = 0 に対するもので、第二成分が BadH = 1 に対するものです。
julia> ranef(model2)
1-element Vector{Matrix{Float64}}:
[-0.5729340987395385 0.5729340987053914]
各モデルの推定値を計算した結果が以下です (適宜コメントを書いています)。
# GLM の BadH = 0 に対応する推定値
julia> [1, 0]' * coef(model1)
0.6616209295796434
# GLM の BadH = 1 に対応する推定値
julia> [1, 1]' * coef(model1)
1.81091996698979
# GLMM の推定値
julia> fixef(model2)[1] .+ ranef(model2)[1][1, :]
2-element Vector{Float64}:
0.6620068635613853
1.8078750610063152
わりと同じような結果が得られていますね。
数式上に違いがあるのは当たり前ですが、これくらいのシンプルな例だと使い分けが難しいです。他にもいろいろ考えてみました。
- カテゴリカル変数 が 3 つ以上のカテゴリーを持つ場合。
- 例えば が曜日だったとしたら、GLM においては月曜ダミーや火曜ダミーを考えることになります。
- その場合、数式上は「月曜かつ火曜」という状況を考えることができてしまいます。
- GLMM ならカテゴリカルな状況を素直に表現できます。
- 他の回帰変数もある場合
- badhealth データには Age もありますから、GLMM を使った場合以下のようなモデリングも可能です。
fit(MixedModel, @formula(NumVisit ~ Age + (1|BadH)))fit(MixedModel, @formula(NumVisit ~ (Age|BadH)))
- GLM では表現できないビジネスロジックを組み込めるのはメリットですね。
- badhealth データには Age もありますから、GLMM を使った場合以下のようなモデリングも可能です。
いくつか考えてはみましたが、パッと思い浮かんだのが GLMM のほうが良いというものだけでした。このあたりについては自分の中で決着がついていないので、引き続き調べたり考えたりしていきたいです。
まとめ
本記事では GLM の進化版である GLMM を Julia でやってみました。緑本には「現実のデータ解析には GLMM が必要」と書かれています。たしかに、観測済みのデータだけでうまいことモデリングできることは稀で、ランダム効果を考慮しなくてはならないことのほうが多いんだろうと思います。そういう意味では GLMM モデリングをさくっとコーディングできるようにはなっておきたいなと思いました。次は階層ベイズモデリングをやっていきます。