Julia で GLM

2022-01-01
JuliaGLM

はじめに

前提知識

GLM (一般化線形モデル) についての理論的背景はある程度前提としています。

参考文献

緑本と呼ばれる データ解析のための統計モデリング入門 を手元に置きながら記事を書いています。

実行環境など

Intel Mac を利用しています。

$ sw_vers
ProductName:	Mac OS X
ProductVersion:	10.15.7
BuildVersion:	19H2

Julia のバージョンは 1.7 です。

$ julia -v
julia version 1.7.0

準備

Julia は Homebrew 経由でインストールできます。

$ brew install --cask julia

適当なディレクトリを作成し、julia の REPL を起動します。

$ mkdir ~/glm
$ cd ~/glm
$ julia
julia>

ここで ] を押すと、Pkg モードになり、プロンプトが変わります。 そこで activate . とすることで、そのディレクトリがプロジェクトルートになり、さらにプロンプトが変わります。

(@v1.7) pkg> activate .
  Activating new project at `~/glm`

(glm) pkg>

必要なパッケージをインストールします。パッケージ名はコンマ区切りでも良いです。

(glm) pkg> add DataFrames Distributions GLM Plots RDatasets StatsBase StatsModels StatsPlots
パッケージ説明
DataFramesデータフレーム
Distributions確率分布
GLM一般化線形モデルを扱うためのパッケージ
Plotsグラフ描画
RDatasetsR 言語に標準搭載されているデータセットを Julia から利用できるようにしたパッケージ
StatsBase統計にかかわる基本的な関数群が提供されているパッケージ
StatsModels線形予測子を記述するためのパッケージ
StatsPlotsPlots に機能が追加されたパッケージ。確率分布のグラフ描画などが可能

インストール終了後 st と入力することで、パッケージの一覧を見ることができます。

(glm) pkg> st
      Status `~/Project.toml`
  [a93c6f00] DataFrames v1.3.1
  [31c24e10] Distributions v0.25.37
  [38e38edf] GLM v1.5.1
  [91a5bcdd] Plots v1.25.2
  [ce6b1742] RDatasets v0.7.6
  [2913bbd2] StatsBase v0.33.13
  [3eaba693] StatsModels v0.6.28
  [f3b207a7] StatsPlots v0.14.30

バックスペースを押すことで通常モードに戻ります。各種パッケージを読み込んでおきましょう。こちらはコンマ区切りです。

julia> using DataFrames, Distributions, GLM, RDatasets, Statistics, StatsBase, StatsModels, StatsPlots

これで準備完了です。

ちなみに Ctrl+D 等で REPL を抜けられますが、再びプロジェクトローカルな REPL を起動するには julia --project コマンドを実行します。

GLM

利用するデータ

RDatasets で利用できるデータを見てみます。

julia> RDatasets.packages()
34×2 DataFrame
 Row │ Package       Title
     │ String15      String
─────┼─────────────────────────────────────────────────
   1 │ COUNT         Functions, data and code for cou…
   2 │ Ecdat         Data sets for econometrics
   3 │ HSAUR         A Handbook of Statistical Analys…
   4 │ HistData      Data sets from the history of st…

緑本の Poisson 回帰を参考に進めていきたいので、カウントデータを使いたいです。ひとつめの COUNT を見てみましょう。

julia> RDatasets.datasets("COUNT")
15×5 DataFrame
 Row │ Package   Dataset     Title       Rows   Columns
     │ String15  String31    String      Int64  Int64
─────┼──────────────────────────────────────────────────
   1 │ COUNT     affairs     affairs       601       18
   2 │ COUNT     azdrg112    azdrg112     1798        4
   3 │ COUNT     azpro       azpro        3589        6
   4 │ COUNT     badhealth   badhealth    1127        3
   5 │ COUNT     fasttrakg   fasttrakg      15        9

ここでは badhealth を使ってみることにします。

julia> data = dataset("COUNT", "badhealth")
1127×3 DataFrame
  Row │ NumVisit  BadH   Age
      │ Int64     Int64  Int64
──────┼────────────────────────
    1 │       30      0     58
    2 │       20      0     54
    3 │       16      0     44
    4 │       20      0     57

全部で 3 つのカラムがあります。RDocumentation を見ると、ドイツの医療関係のデータということはわかりますが、詳しいカラムの説明は無いですね。おそらくですが以下のようなデータだと思われます。

  • NumVisit (整数): 病院への通院回数
  • BadH (0 or 1): 健康状態
  • Age (整数): 年齢

可視化

まずは可視化から始めましょう。NumVisit がどんな分布なのかをヒストグラムで表示してみます。

julia> histogram(data.NumVisit)
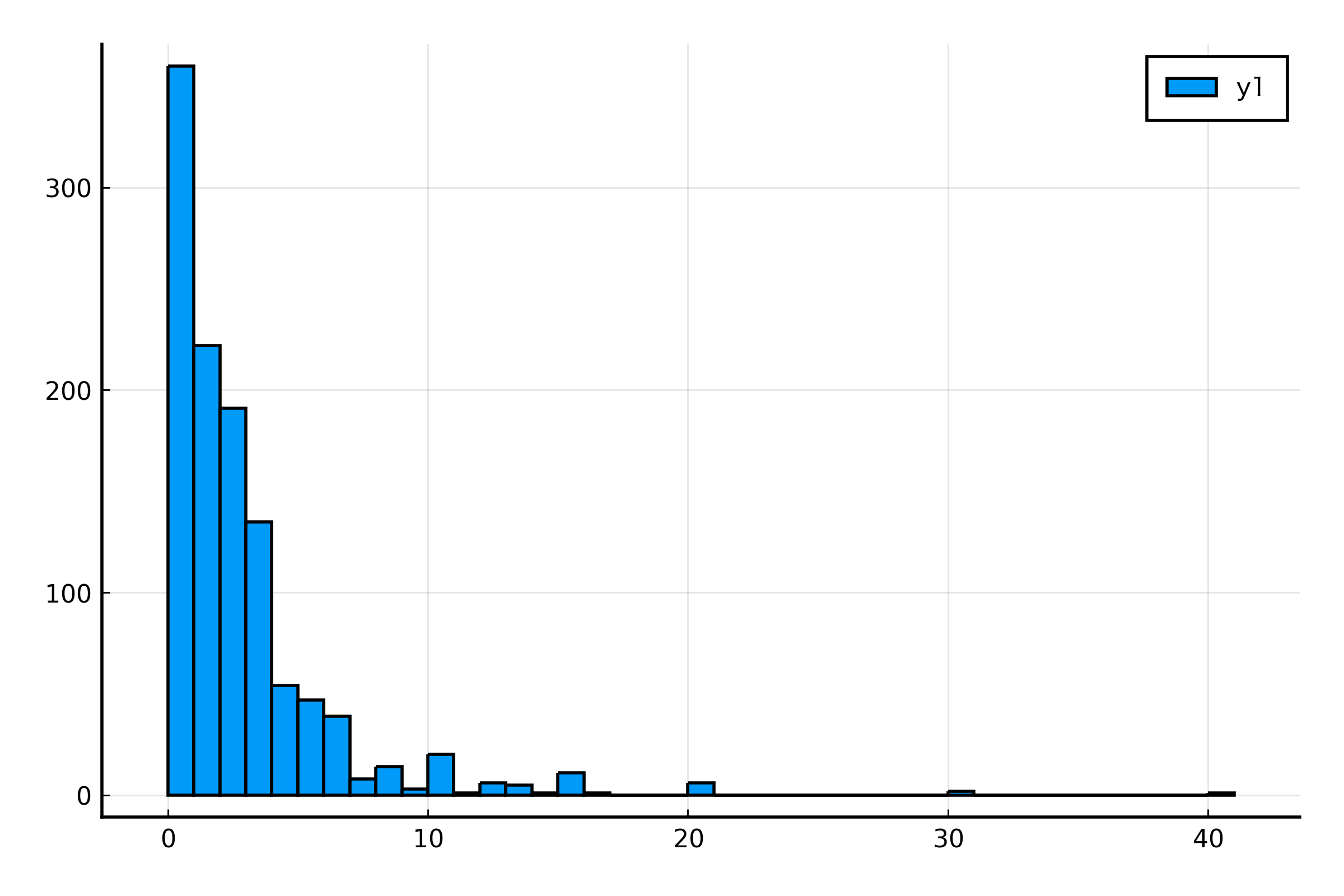
NumVistのヒストグラム

Poisson 分布へのあてはめを考えているため、Poisson 分布と一緒に表示してみます。そのためにヒストグラムを正規化しし、左に 0.5 だけ並行移動させるために bins パラメータを設定しています。また、Poisson 分布の平均パラメータは標本平均にしています。

julia> histogram(data.NumVisit, norm=true, bins=-0.5:1:(maximum(data.NumVisit) + 0.5))
julia> plot!(Poisson(mean(data.NumVisit)), t=:line, lw=2)
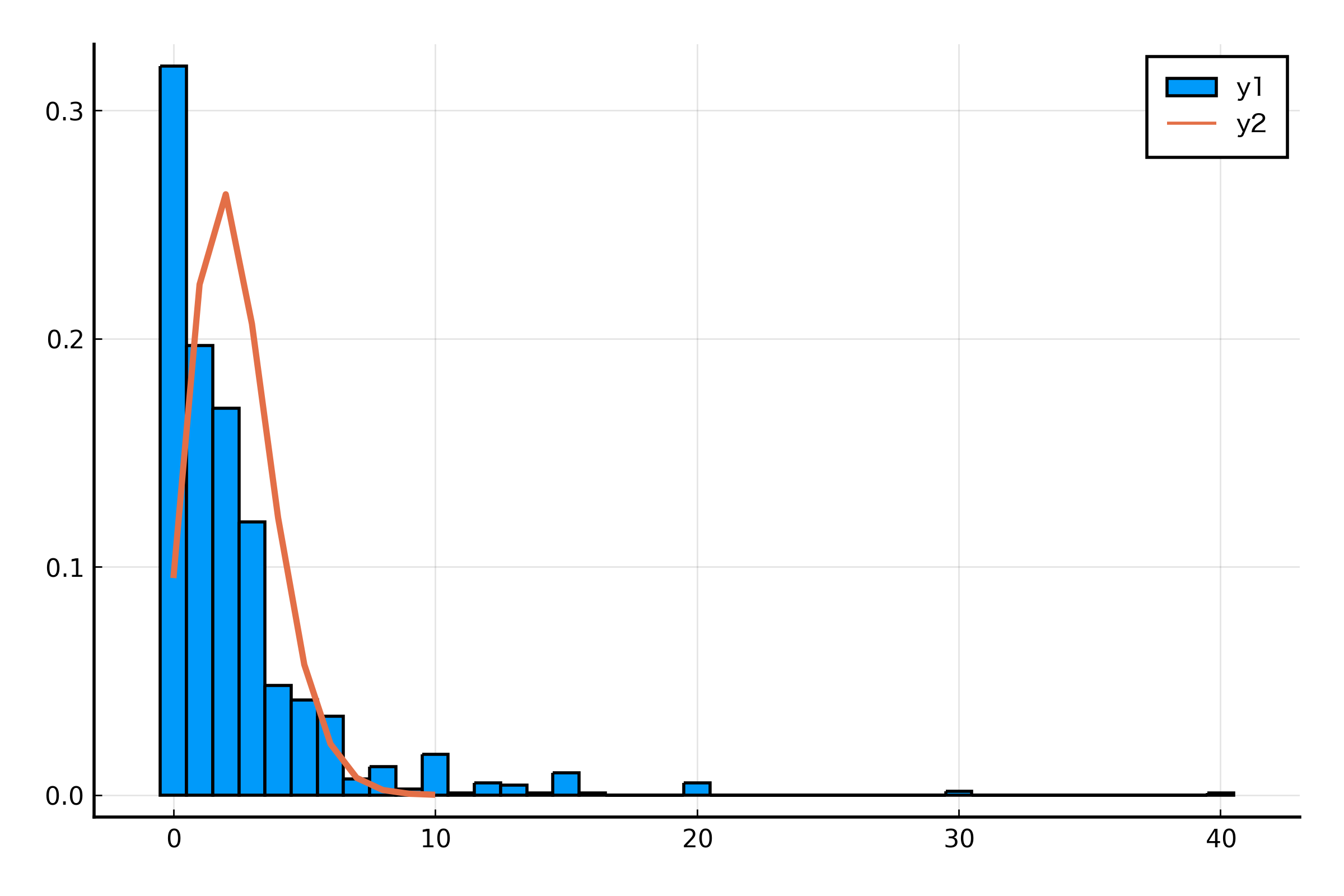
NumVistのヒストグラムとPoisson分布

最後にテキストと同じように散布図も描いてみましょう。点を重ねないように描画しているようで、その分ずれて表示されている点もありそうな感じがします。

julia> plot(data.Age, data.NumVisit, group=data.BadH, t=:scatter, xaxis="Age", yaxis="NumVisit")
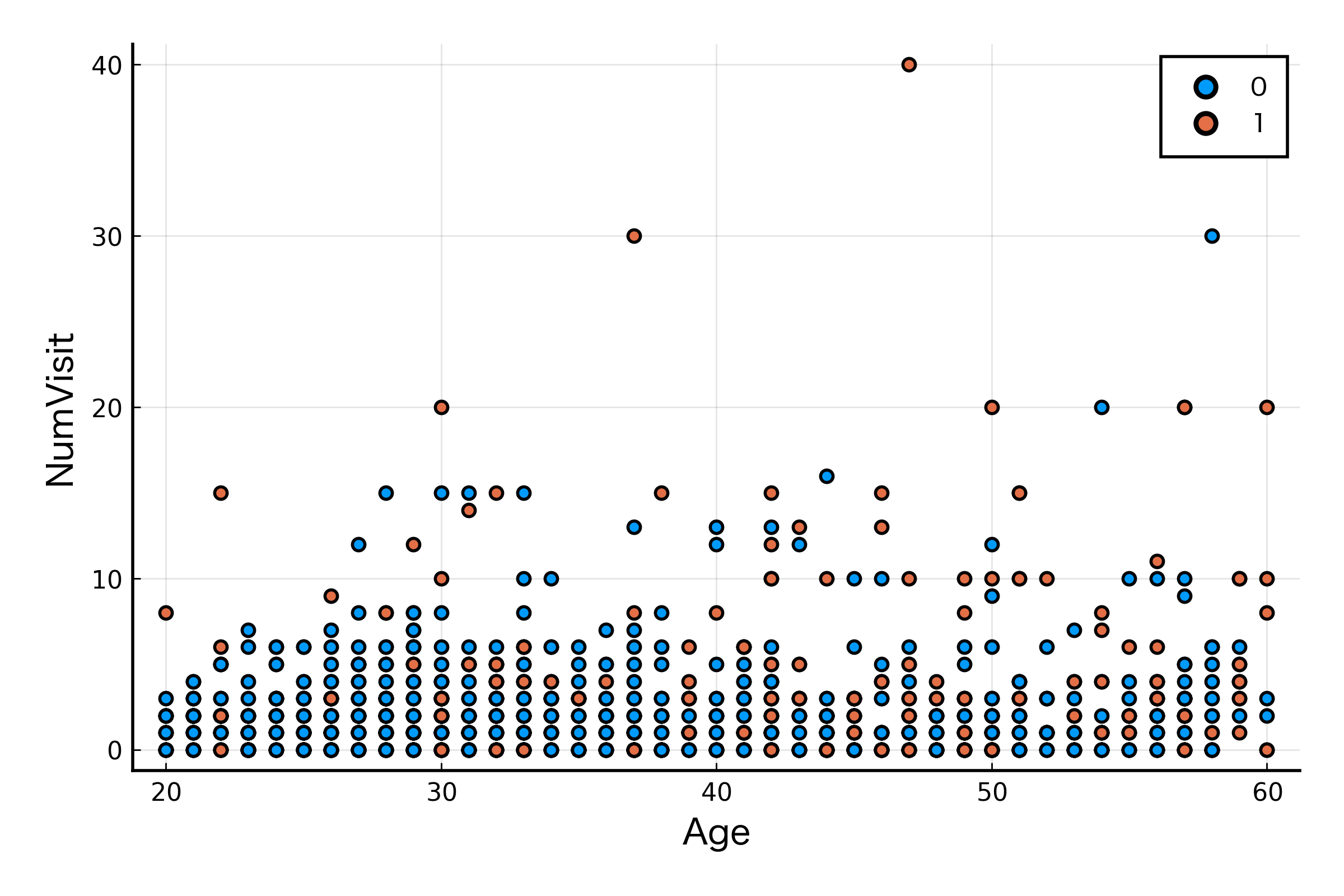
NumVistの散布図

Age を固定したとき、BadH が 1 のほうが NumVisit が大きいように見えますね。年齢を重ねるごとに NumVisit が大きくなるかというと、そうでもなさそうに見えます。

代表値

まずは可視化を通してデータの雰囲気を掴みました。次に NumVisit の平均と分散を調べてみます。平均は Statistics パッケージの mean 関数、分散は同パッケージの var 関数で計算できます。

実行例は以下です。末尾にセミコロン ; を打つことで badh の中身が出力されなくなります。

julia> badh = filter(row -> row.BadH == 1, data);

julia> mean(badh.NumVisit)
6.116071428571429

julia> var(badh.NumVisit)
41.2206402831403
NumVisit平均分散
全体2.35311.987
BadH = 01.9377.056
BadH = 16.11641.220

やはり BadH が 1 であるほうが、NumVisit は大きくなる傾向にあるようです。

説明変数なし

まずは説明変数なしで Poisson 分布にあてはめてみます。つまり NumVisit が以下のように生成されていると仮定するということです。

NumVisit∼Pois(λ)\mathrm{NumVisit} \sim \mathrm{Pois}(\lambda)

この場合 λ\lambda の最尤推定値は標本平均に一致するのですが、GLM パッケージを使うことでそれを確かめてみましょう。

julia> fit = glm(@formula(NumVisit ~ 1), data, Poisson(), IdentityLink())
NumVisit ~ 1

Coefficients:
───────────────────────────────────────────────────────────────────────
               Coef.  Std. Error      z  Pr(>|z|)  Lower 95%  Upper 95%
───────────────────────────────────────────────────────────────────────
(Intercept)  2.35315   0.0456944  51.50    <1e-99    2.26359    2.44271
───────────────────────────────────────────────────────────────────────

Poisson 分布の平均値パラメータの最尤推定値 (2.35315) は上で計算しておいた標本平均と一致していますね。

説明変数あり

次に説明変数を追加してみましょう。リンク関数にはして対数リンク関数を使うことにします。

まずは Age だけを追加します。

julia> fitAge = glm(@formula(NumVisit ~ Age), data, Poisson(), LogLink())
NumVisit ~ 1 + Age

Coefficients:
────────────────────────────────────────────────────────────────────────
                 Coef.  Std. Error     z  Pr(>|z|)  Lower 95%  Upper 95%
────────────────────────────────────────────────────────────────────────
(Intercept)  0.290283   0.0712965   4.07    <1e-04  0.150544    0.430021
Age          0.0148371  0.00175866  8.44    <1e-16  0.0113902   0.018284
────────────────────────────────────────────────────────────────────────

次は BadH だけを追加します。

julia> fitH = glm(@formula(NumVisit ~ BadH), data, Poisson(), LogLink())
NumVisit ~ 1 + BadH

Coefficients:
────────────────────────────────────────────────────────────────────────
                Coef.  Std. Error      z  Pr(>|z|)  Lower 95%  Upper 95%
────────────────────────────────────────────────────────────────────────
(Intercept)  0.661621   0.0225466  29.34    <1e-99    0.61743   0.705812
BadH         1.1493     0.0443643  25.91    <1e-99    1.06235   1.23625
────────────────────────────────────────────────────────────────────────

次は Age と BadH の両方です。

julia> fitAgeH = glm(@formula(NumVisit ~ Age + BadH), data, Poisson(), LogLink())
NumVisit ~ 1 + Age + BadH

Coefficients:
───────────────────────────────────────────────────────────────────────────
                  Coef.  Std. Error      z  Pr(>|z|)  Lower 95%   Upper 95%
───────────────────────────────────────────────────────────────────────────
(Intercept)  0.447022    0.071428     6.26    <1e-09  0.307025   0.587018
Age          0.00582202  0.00182218   3.20    0.0014  0.0022506  0.00939343
BadH         1.10833     0.0461695   24.01    <1e-99  1.01784    1.19882
───────────────────────────────────────────────────────────────────────────

最後に Age と BadH の交互作用も含めて考えてみます。NumVist ~ Age * BadH の部分は NumVisit ~ Age + BadH + Age & BadH と書いても同じです。

julia> fitAgeHInt = glm(@formula(NumVisit ~ Age * BadH), data, Poisson(), LogLink())
NumVisit ~ 1 + Age + BadH + Age & BadH

Coefficients:
───────────────────────────────────────────────────────────────────────────────
                   Coef.  Std. Error      z  Pr(>|z|)    Lower 95%    Upper 95%
───────────────────────────────────────────────────────────────────────────────
(Intercept)   0.346885    0.0814122    4.26    <1e-04   0.18732      0.50645
Age           0.00850303  0.00208567   4.08    <1e-04   0.00441521   0.0125909
BadH          1.56895     0.181531     8.64    <1e-17   1.21316      1.92474
Age & BadH   -0.0109177   0.0041956   -2.60    0.0093  -0.019141    -0.00269452
───────────────────────────────────────────────────────────────────────────────

ここまで 5 つのモデルを見てきましたが、どれが一番良いモデルなのでしょうか？テキストと同様に AIC でもって比較してみます。StatsBase の aic 関数を使って計算した結果をまとめました。loglikelihood 関数と変数の数を使って自分で計算したものとちょっと値が違うのですが一旦気にしないでおきましょうかね。

モデルAIC
fit6190
fitAge6121
fitH5646
fitAgeH5638
fitAgeHInt5633

AIC によってモデル選択をするなら、fitAgeHInt が最も良いということになりそうですね。ただ交互作用を含むモデルは解釈が難しいため、fitAgeH のほうが実用的には使い勝手が良さそうです。

まとめ

データ可視化、代表値の計算、GLM モデリング、AIC によるモデル選択を一通りやってみました。実務でさくっと試してみるくらいはできそうです。