コンパクト生成空間の圏

2019-02-27 math トポロジー, 位相

コンパクト生成空間の圏についてまとめた.

以下空間は基本的にHausdorffとする.

参考文献

本記事はGrayのHOMOTOPY THEORYという本を参考にした.

定義

まず定義から.

定義空間\(X\)(もちろんHausdorff)がコンパクト生成(compactly generated)空間であるとは, 全てのコンパクト集合からなる集合族に関して弱位相を持つことである. コンパクト生成空間と連続写像からなる圏を\(\mathcal{CG}\)と表すことにする.

任意の空間\(X\)に対し, コンパクト部分集合族に関する弱位相を入れ直すことで, コンパクト生成空間が出来上がる. これを\(k(X)\)と表すことにすれば, \(k\)は関手\(k: \mathcal{H} \to \mathcal{CG}\)を定める(詳細は後述). ただし\(\mathcal{H}\)はHausdorff空間からなる圏である.

この圏で考えるとなにが嬉しいのかを先に述べておく.

  • この記事でコンパクト開位相に関する命題をいくつか紹介したが, そのなかで局所コンパクト性を仮定するものがあった. でも\(\mathcal{CG}\)で考えればその仮定は必要なくなる.

  • コンパクト部分集合に関する弱位相が入っているから, 写像\(f:X\to Y\)が連続かどうかは, 各コンパクト部分集合\(C\subset X\)上で連続であることを確認すれば十分.

便利な圏だからといって, そんなに制限があるわけでもない.

  • \(\mathcal{CG}\)は多くの位相空間を含む. 例えば局所コンパクト空間や, 第一可算公理を満たす空間などである. つまりCW複体はコンパクト生成空間である.

  • \(X\)と\(k(X)\)の違いはあまりない. 実際両者のホモトピー群は同型である.

準備

補題 \(X\in \mathcal{CG},\ Y\in \mathcal{H}\)とする. 写像\(f:X\to Y\)が連続であるための必要十分条件は, 各コンパクト集合\(C\subset X\)に対し, \(f|_C\)が連続となることである.

証明 弱位相だから当たり前.

命題

  1. \(X\in \mathcal{CG}\)とし, \(A\subset X\)を閉集合とすると, \(A\in\mathcal{CG}\)である.
  2. \(X\in \mathcal{CG},\ Y\in\mathcal{H}\)とし, \(f:X\to Y\)を商写像とすると, \(Y\in \mathcal{CG}\)である.

つまり以下のようなことが\(\mathcal{CG}\)の中で議論できるということである. \[ A\hookrightarrow X \to X/A \]

\(k\)が関手であること

定理 \(k\)は\(\mathcal{H}\)から\(\mathcal{CG}\)への関手である.

証明 まず\(k(X)\in \mathcal{CG}\)であることを次のステップに従って証明する.

  1. 恒等関数\(I:k(X)\to X\)は連続である.
  2. \(k(X)\in \mathcal{H}\).
  3. \(k(X)\)と\(X\)は同じコンパクト集合を持つ.
  4. \(k(X)\in\mathcal{CG}\).

では順次証明していこう.

  1. 定義から\(k(X)\)は\(X\)よりも多くの開集合を持っているから明らか.
  2. \(X\in\mathcal{H}\)であり, \(k(X)\)のほうが多くの開集合を持っているのだから明らか.
  3. コンパクト集合の連続像はコンパクトであるから, \(k(X)\)のコンパクト集合は\(X\)においてもコンパクトである. もっと直感的に, \(k(X)\)は\(X\)よりも多くの開集合を持っているのだから, \(k(X)\)のほうがコンパクトになりにくい環境である. したがって\(k(X)\)のほうがコンパクト集合は少ない. 逆を証明する. \(C\subset X\)をコンパクトとし, \(C' = I^{-1}(C)\)とする. 結局\(C' \to C\)の逆写像が連続であることを証明すればよい. \(B\subset C'\)を閉集合とすると, コンパクト生成位相の定義から, \(X\)の任意のコンパクト集合と\(B\)の共通部分は閉集合である. 特に\(B\cap C = B\)は\(X\)において閉集合である. これは\(C'\to C\)が連続であることを意味する.
  4. \(A\subset k(X)\)は\(k(X)\)任意のコンパクト集合との共通部分が閉集合であるとする. 3より, \(A\)は\(X\)の任意のコンパクト集合との共通部分が閉集合である. コンパクト生成位相の定義から, \(A\)は\(k(X)\)において閉集合である. これは\(k(X)\in \mathcal{CG}\)を意味する.

最後の命題から, \(X\in\mathcal{CG}\)のとき\(I:k(X)\to X\)は同相写像であることも分かる. 次に写像についてみていく.

\(f: X\to Y \in \mathcal{H}\)とする. 集合同士の関数として\(k(f)=f\)とする. これが\(\mathcal{CG}\)において連続であることが証明できれば, \(k\)が関手であることがわかる.

\(k(f)\)の連続性は, 各コンパクト集合\(C\subset X\)上で確認すれば十分であるが, \(k(f)|_C\)は次のように分解できる. \[ C\cong I(C) \to f(I(C))\cong f(C)\] 各写像が連続であるから, \(k(f)|_C\)も連続である.

積

\(\mathcal{H}\)におけるproductを\(X\times_c Y\), \(\mathcal{CG}\)におけるproductを\(X\times Y\)と区別して書くことにする.

定理\(X\times Y = k(X\times_c Y)\)

つまり\(\mathcal{CG}\)におけるproductは, 一旦\(\mathcal{H}\)でproductをとってから関手\(k\)で移したものであるということ.

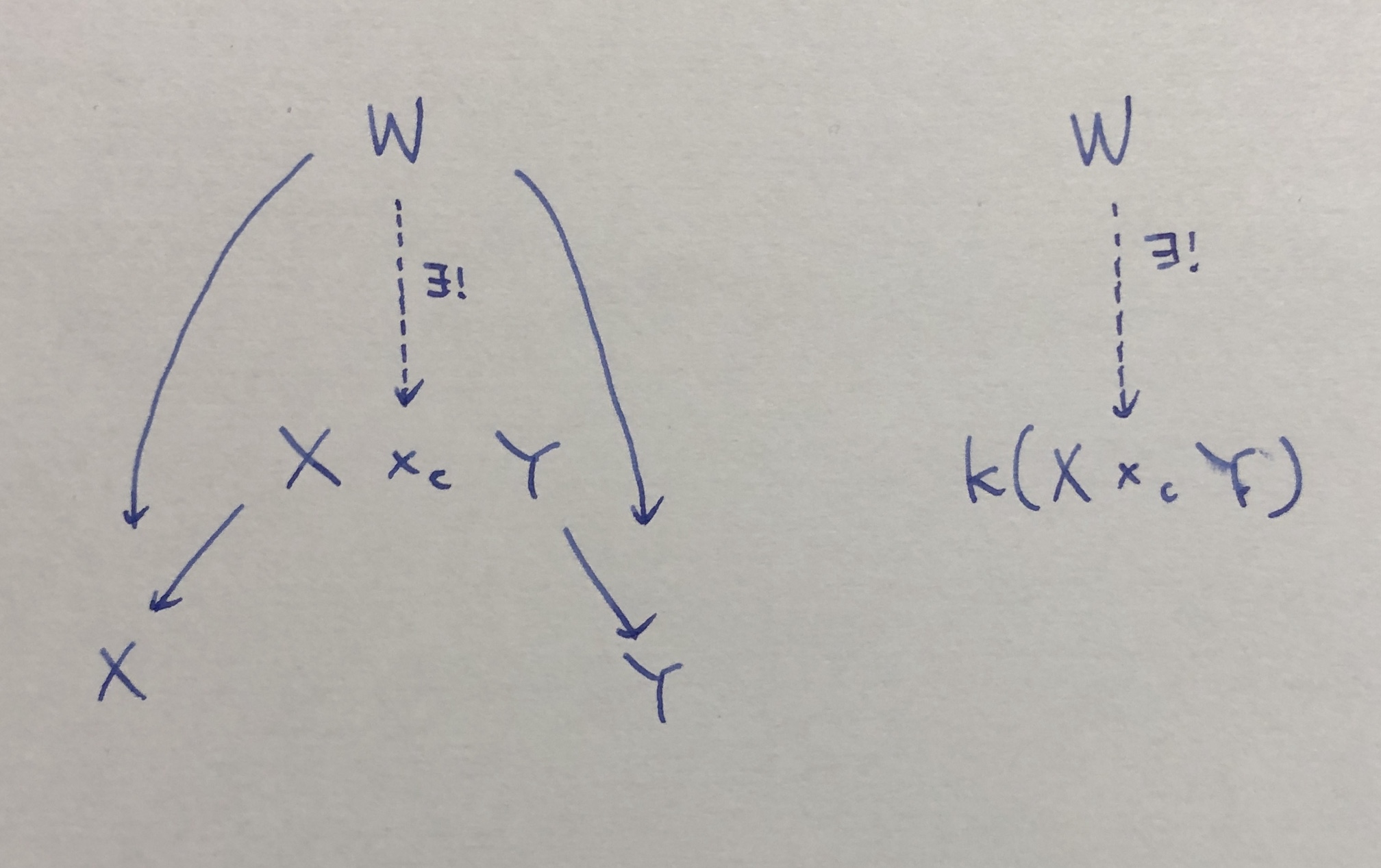
証明productのuniversal propertyを証明する. 2つの射\(W\to X,\ W\to Y\)があると, 圏\(\mathcal{H}\)で考えたときに射\(W\to X\times_c Y\)が一意に定まる. これを関手\(k\)で送ると射\(W\to k(X\times_c Y)\)が得られる(\(k(W) = W\)であることに注意). この射の一意性も少し考えるとわかる.

命題\(X\)を局所コンパクト空間, \(Y\in\mathcal{CG}\)とすると, \(X\times Y = X\times_c Y\).

命題\(X,Y\in\mathcal{H}\)とすると, \(k(X)\times k(Y) = k(X \times_c Y)\)

ホモトピー群

定理\(I: k(X)\to X\)により誘導される写像\(I_*:\pi_n(k(X), *) \to \pi_*(X, *)\)は全単射である.

証明\(\phi : (S^n, *)\to (X, *)\)のホモトピー類に対し\(k(\phi)\)のホモトピー類を対応させる写像が\(I_*\)の逆写像である.

ちなみにこれがwell-definedであることは, 関手\(k\)がホモトピーを保つかどうかを考えればよい.

\(H: X\times_c I \to Y\)が\(f\)から\(g\)へのホモトピーであるとする(\(I\)は単位区間です…紛らわしいね). これまでに挙げた命題から

\[ k(X\times_c I) = k(X)\times k(I) = k(X)\times I \]

であるから,

\[ k(H) : k(X)\times I \to k(Y) \]

である. これは\(k(f)\)から\(k(g)\)へのホモトピーになっている.