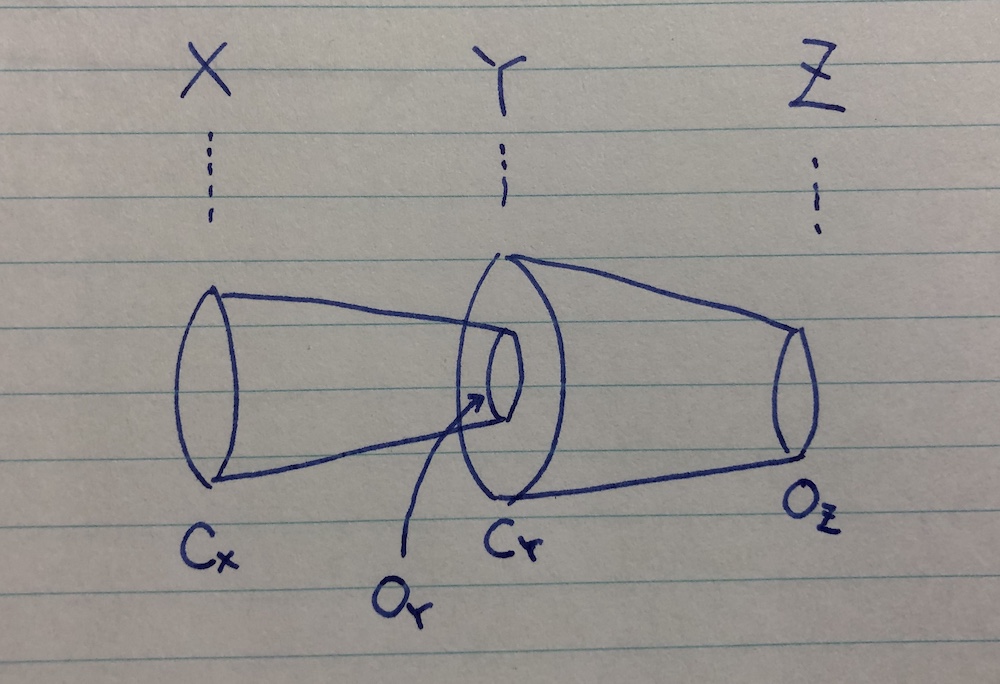コンパクト開位相まとめ

断りがなければ基本 $O, U, V$ は開集合、 $C$ はコンパクトです。適宜証明に合うように読み取ってください。

定義

コンパクト開位相とは、空間 $X$ から空間 $Y$ への連続写像全体 $M(X, Y)$ に定義される位相である。

定義

コンパクト集合 $C\subset X$ と開集合 $O\subset Y$ に対し、

W(C, O) = \{f : X\to Y \mid f(C)\subset O\}

と定義する。 $W(C, O)$ 全体からなる部分集合族から生成されるのが、コンパクト開位相である。

コンパクト開位相は開基ではない

開基とは

位相の部分集合。ベクトル空間でいうところの基底みたいなもの。全ての開集合は開基の組み合わせでできる。ちゃんと説明する。

定義位相の部分集合 $\mathcal{B}\subset \mathcal{O}$ が開基とは、以下を満たすことである。

任意の開集合 $O\in \mathcal{O}$ に対し、部分集合族 $\mathcal{B}_0\subset \mathcal{B}$ が存在し、

O = \bigcup\mathcal{B}_0

が成り立つ。

開基について次の事柄が知られている。

命題集合 $X$ の部分集合族 $\mathcal{B}$ が、 $X$ のある位相の開基となるためには、以下の2条件が必要十分である。

$X = \bigcup \mathcal{B}$
任意の $B_1, B_2\in \mathcal{B}$ と $x \in B_1\cap B_2$ に対し、 $B\in \mathcal{B}$ が存在し、

x \in B \subset B_1\cap B_2

が成り立つ。

コンパクト開位相が開基ではないこと

2つの離散空間 $X = \{0, 1\},\ Y = \{a, b\}$ に対し、 $B_1 = W(0,a),\ B_2 = W(1, b)$ とすればよい。 $B_1\cap B_2$ の元はひとつしかないが、この元に対して開基の条件を満たすような $B$ は存在しない。

準開基とは

開基に似たような概念として、準開基がある。これは開基よりも条件を弱めたもの。準開基がベクトル空間における基底なら、開基は正規直交基底みたいな感じ？

定義 $(X, \mathcal{O})$ を位相空間とする。位相の部分集合 $\mathcal{T}\subset \mathcal{O}$ が準開基であるとは, 次を満たすことである。

任意の開集合 $O\in \mathcal{O}$ と $x\in O$ に対し、有限個の元 $N_1,\ldots ,N_r\in \mathcal{T}$ が存在し、

x \in N_1\cap\cdots\cap N_r \subset O

が成り立つ。

集合 $X$ と部分集合族 $\mathcal{T}$ に対し、 $\mathcal{T}$ を準開基とするような $X$ の位相が一意に定まる。それを $\mathcal{T}$ で生成される位相という (上で既にこの言葉使っちゃってるけど)。

写像の連続性を証明するには準開基の元を調べれば十分。つまりは以下が成り立つ。

命題 $f: X\to Y$ が連続 $\iff$ 任意の準開基の元 $N\subset Y$ に対し、 $f^{-1}(N)$ が $X$ の開集合

証明 $(\Rightarrow)$ は当たり前なので $(\Leftarrow)$ を証明する。任意に開集合 $O\subset Y$ と $x\in f^{-1}(O)$ をとる。連続性を証明するには、 $x$ の近傍 $U$ であって $f(U)\subset O$ となるものの存在を示せばよい。準開基の定義から、有限個の準開基の元 $N_1,\ldots , N_r$ が存在し、

f(x)\in N_1\cap\cdots\cap N_r \subset O

が成り立つ。 $U =f^{-1}(N_1\cap\cdots\cap N_r)$ とすればよい。

いくつかの命題

命題の証明に使う補題を用意しておく。

補題局所コンパクト空間 $Y$ に対し、 $C$ をコンパクト集合、 $U$ を $C$ の近傍とする。するとコンパクトな近傍 $C\subset D\subset U$ が存在する。

証明局所コンパクトというのは各点が対しコンパクトな近傍を持つことであるけれど、実はコンパクト集合も同様の性質を持つのである。

まず局所コンパクト性から、各点 $y\in C$ はコンパクトな近傍 $y\in D_y\subset U$ を持つ。すると集合族 $\{mathrm{int}(D_y)\}_{y\in C}$ は $C$ の開被覆となる。 $C$ はコンパクトであるから、有限個の $y_1,\ldots ,y_n$ における近傍で $C$ が覆える。すると $D$ は以下で定義できる。

D = \bigcup_{i=1}^n D_{y_i}

ではコンパクト開位相に関する命題へ移ろう。

命題 $Y$ が局所コンパクトであるとき、写像の合成により定義される写像

T: M(X, Y) \times M(Y, Z) \to M(X, Z)

は連続である。

証明コンパクト集合 $C\subset X$ と開集合 $O\subset Z$ に対し、準開基の元 $W(C, O)$ を考える。また、写像 $f\in M(X, Y),\ g\in M(Y, Z)$ は、 $T(f,g) = g\circ f \in W(C, O)$ を満たすとする。証明すべきは、

(f, g)\in W(C_X, O_Y)\times W(C_Y, O_Z)\subset T^{-1}(W(C, O))

を満たすような $f, g$ の近傍の存在である。しかもこんな風になっていなければならない。

天下り的ではあるが、次のようにすればうまくいく。

$C_X = C$
$O_Y = \mathrm{int}(C_Y)$
$C_Y =$ 上の補題において $C$ を $f(C)$ に、 $U$ を $g^{-1}(O)$ に置き換えたときの $D$
$O_Z = O$

写像 $f: X\times Y \to Z$ に対し写像 $g:X\to M(Y,Z)$ を次のように定義する。

f(x,y) = g(x)(y)

これらの写像について以下が成り立つ。

命題

$f$ が連続ならば $g$ も連続である。
$g$ が連続で $Y$ が局所コンパクトであるとき、 $f$ も連続である。

証明そもそも $g(x)$ は連続なの？(言い換えると $g(x)\in M(Y,Z)$ なの？)という疑問があるかもしれないが、それは $g(x)$ が次の合成写像であることを考えると明らか。

\{x\} \times Y \to X\times Y \to Z

では命題を証明していく。

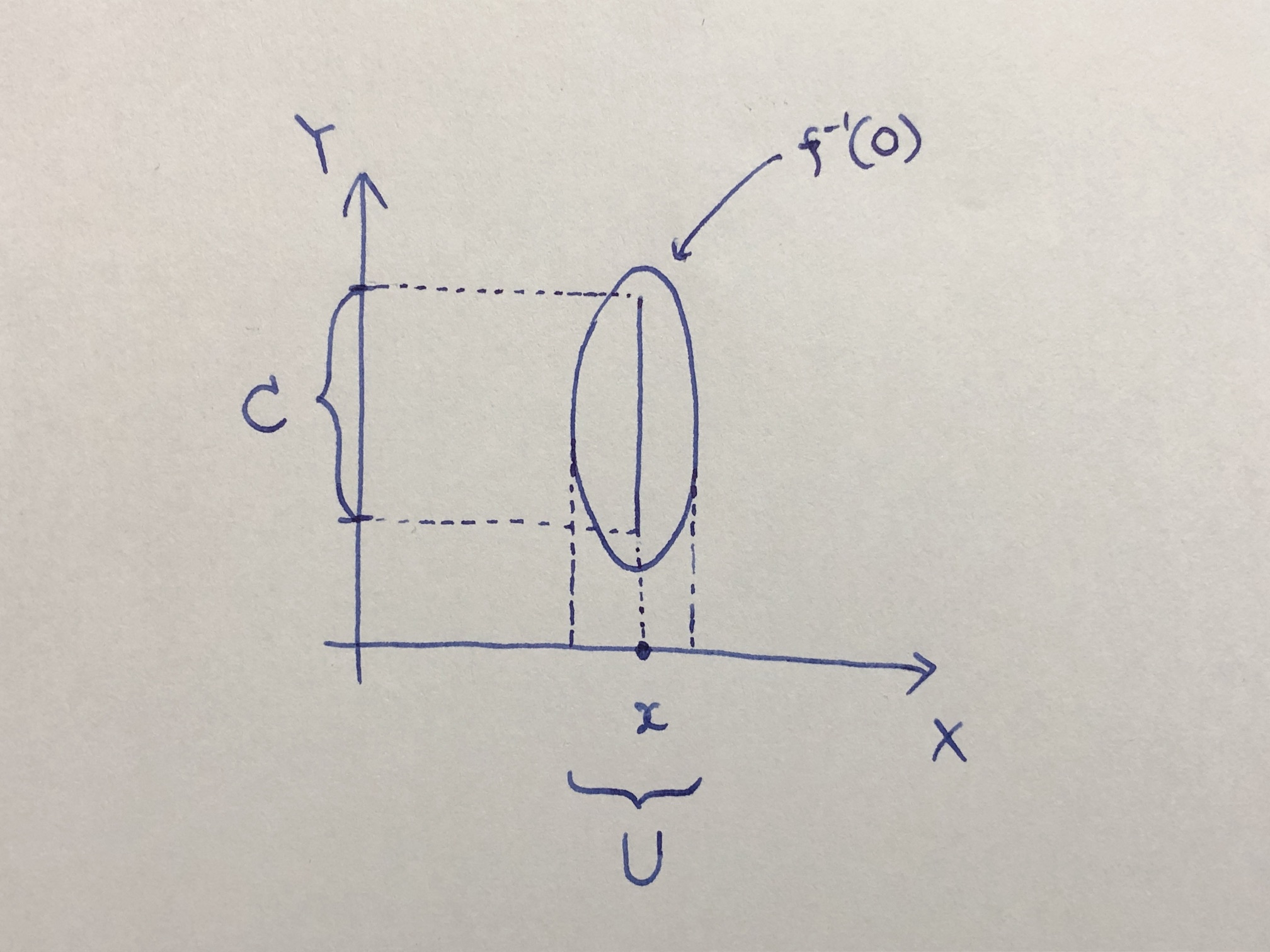
$x\in X$ に対し $f(x)\in W(C, O)\subset M(Y,Z)$ が成り立つとする。つまりこんな状況である。

$f(\{x\}\times C) \subset O$

これを次のように太らせてもいいことを証明したい。

f(U\times C) \subset O

まずは間違った証明から。

$f$ は連続だから $f^{-1}(O)$ は $\{x\}\times C$ を含む開集合である。 $f^{-1}(O)$ の $X$ への射影を $U$ とすればよい。

この証明が間違いであることは、次のような状況を考えると分かる。このような状況だと、 $U\times C$ が $f^{-1}(O)$ からはみ出てしまう。

ではどうすればいいか。 $C$ のコンパクト性を使おう。

$f$ は連続だから、各 $y\in C$ に対し点 $(x,y)$ の近傍 $U_y\times V_y$ が存在し、次を満たす。

(x,y)\in U_y\times V_y \subset f^{-1}(O)

集合族 $\{V_y\}_{y\in C}$ は $C$ の開被覆である。 $C$ はコンパクトであるから、有限被覆 $\{V_{y_i}\}_{i=1}^n$ が取れる。このとき、 $U$ を次のように定義すればよい。

U = \bigcap_{i=1}^n U_{y_i}

$f(x,y)\in O$ とする。 $g(x) : Y\to Z$ は連続であるから $y$ の近傍 $V$ が存在して、

y \in V \subset (g(x))^{-1}(O)

が成り立つ。上の補題から、 $y$ コンパクトな近傍 $C$ で $C\subset V$ となるものが取れる。

今 $g(x)\subset W(C, O)$ まで来た。あとは $x$ を少し太らせることができれば良いが、それは $g$ の連続性から、

x\in U \subset g^{-1}(W(C, O))

となるような $U$ が取れる。

以上から、

(x,y)\in U\times \mathrm{int}(C)\subset f^{-1}(O)

とできたから、 $f$ の連続性が証明できた。