確率変数の最も簡単な例の一つであろうコインの表の出る確率を、2 通りのモデリングでベイズ推論してみました。

状況設定

手元に 1 枚のコインがあるとします。このコインの表の出る確率が知りたいとしましょう。例えばサッカーの公式試合のコイントスに利用したいけど、表と裏の出やすさに偏りがあると困る、みたいな場合です。まあそんな状況でベイズ推論を使おうとする人なんていないでしょうけれど。

さて、このコインを独立に \(N\) 回投げたところ、\(n\) 回だけ表が出ました。このデータをもとに、コインの表の出る確率を推論していきます。

事前分布

表の出る確率 \(q\) の事前分布はベータ分布 \(\mathrm{Beta}(q \mid a, b)\) とします。

次に尤度関数のほうをモデリングしていくわけですが、2 通りの方法を試してみましょう。

二項分布でモデリング

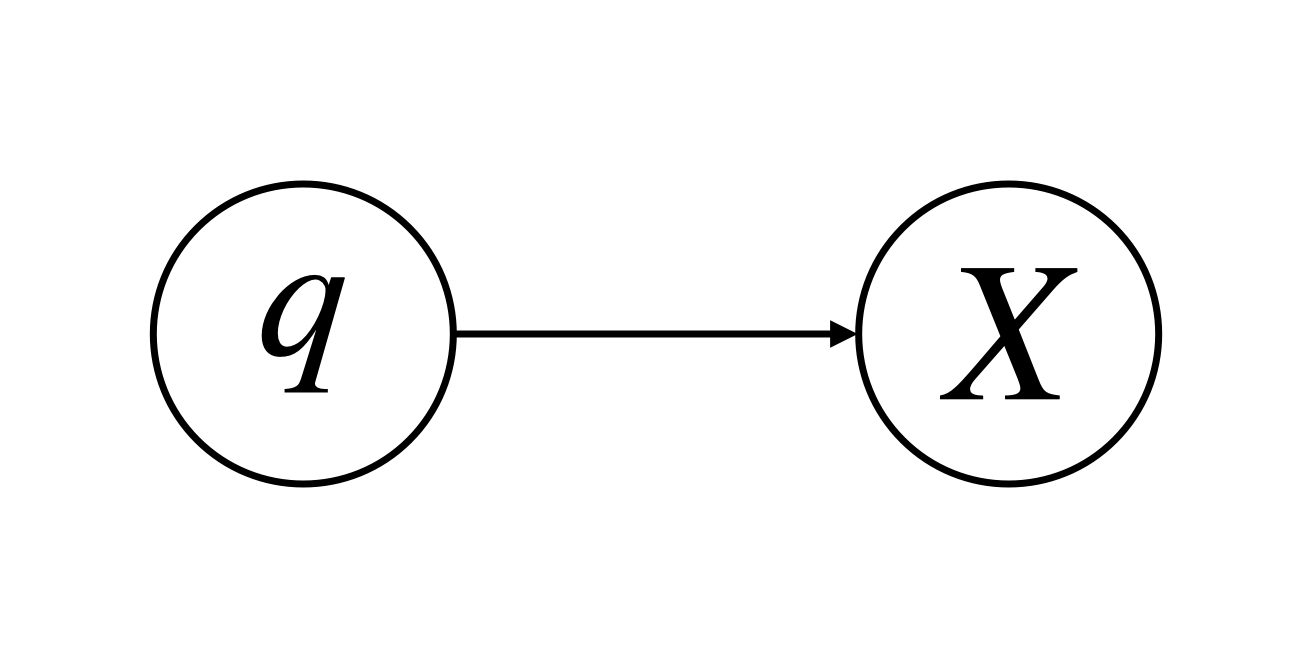
まずは二項分布 \(\mathrm{Binom}(X \mid N, q)\) でモデリングしてみます。つまり、手元のデータは二項分布から得られた一つの標本だと考えるわけです。事前分布とあわせてグラフィカルモデルで表現すると以下のようになります。

必要なものは揃ったので、事後分布を計算していきましょう。チルダは定数倍を除いて等しいこと表しています。

\[ \begin{aligned} p(q \mid X) &= \frac{p(X \mid q)p(q)}{p(X)} \\[.5em] &\sim p(X \mid q)p(q) \\[.5em] &\sim \mathrm{Binom}(X \mid N, q) \cdot \mathrm{Beta}(q \mid a, b) \\[.5em] &= \binom{N}{n} q^n (1-q)^{N-n} \cdot B(a, b)^{-1} q^{a-1} (1-q)^{b-1}\\[.5em] &\sim q^{a+n-1} (1-q)^{b+N-n-1}\\[.5em] &\sim \mathrm{Beta}(a+n, b+N-n) \end{aligned} \]

事後分布もベータ分布になりましたね。事前分布と比べると、第一パラメータに表の出た回数が、第二パラメータに裏の出た回数が足されました。

ベルヌーイ分布でモデリング

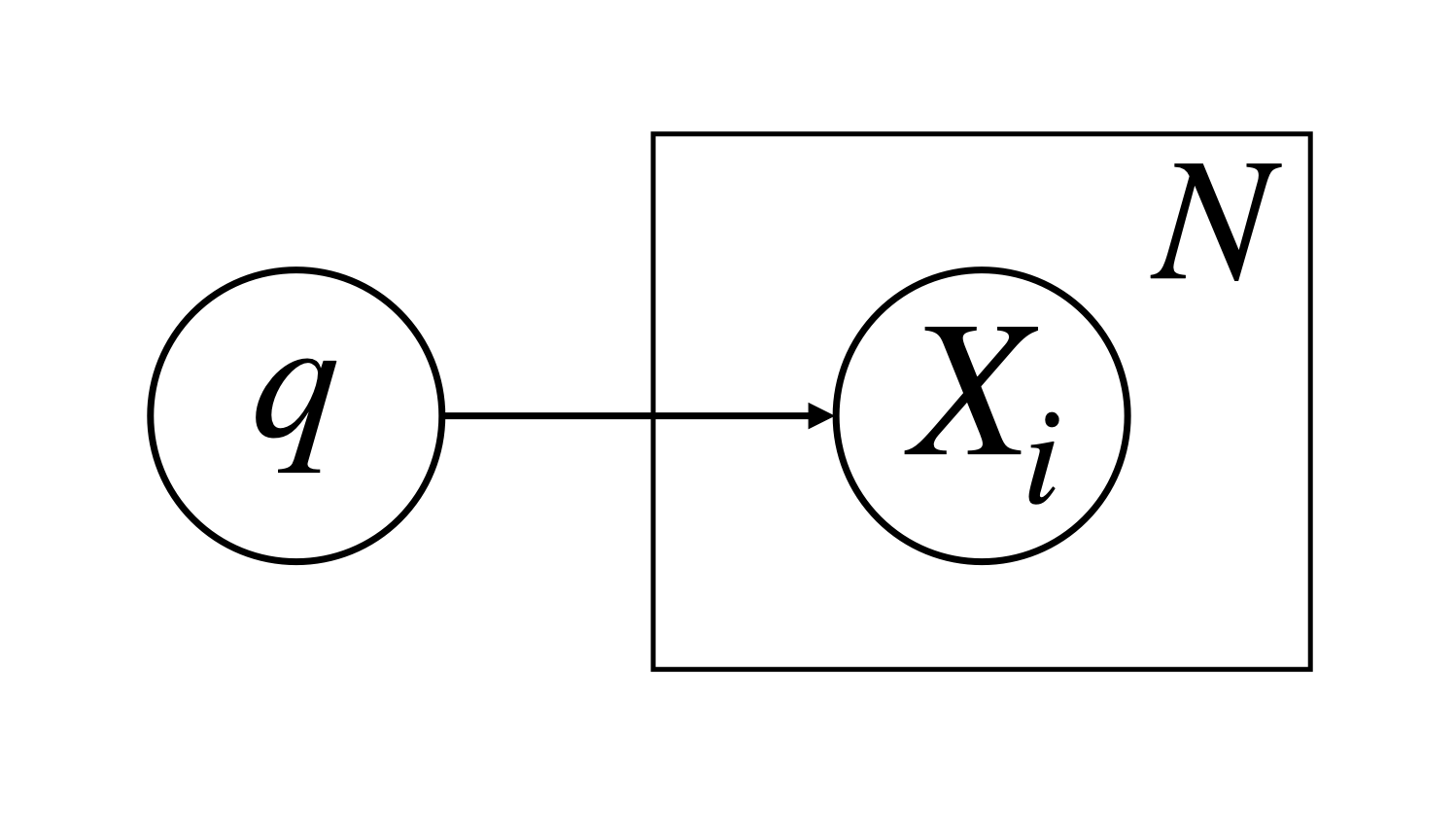
次にベルヌーイ分布 \(\mathrm{Bern}(X_i \mid q)\) でモデリングしてみます。つまり、手元のデータはベルヌーイ分布から得られた \(N\) 個の標本だと考えるわけです。事前分布とあわせてグラフィカルモデルで表現すると以下のようになります。

こちらも事後分布の計算をしていきますが、\(N\) 個のデータを \(\{X_i\}\) のように集合の記法を用いて表しています。

\[ \begin{aligned} p(q \mid \{X_i\}) &\sim \prod_i p(X_i \mid q) \cdot p(q) \\[.5em] &= \prod_i\mathrm{Bern}(X_i \mid q) \cdot \mathrm{Beta}(q \mid a, b) \\[.5em] &\sim q^n (1-q)^{N-n} \cdot q^{a-1} (1-q)^{b-1}\\[.5em] &\sim \mathrm{Beta}(a+n, b+N-n) \end{aligned} \]

というわけで二項分布でモデリングした場合と同様の事後分布が得られました。

まとめ

二項分布でモデリングするか、ベルヌーイ分布の積でモデリングするかの違いは、組み合わせで考えるか順列で考えるかの違いに似てますね。当然二項分布でモデリングするほうが尤度そのものは大きくなります。しかし事後分布に与える情報量としてはどちらでモデリングしても変わらないということなのでした。